Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

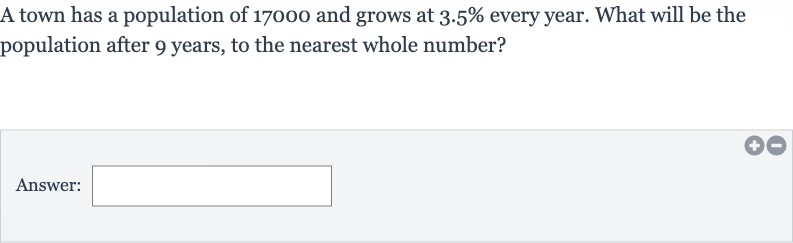
A town has a population of 17000 and grows at
3.5% every year. What will be the population after 9 years, to the nearest whole number?
Answer:

A town has a population of $17000$ and grows at $3.5 \%$ every year. What will be the population after $9$ years, to the nearest whole number? $\newline$ Answer:

View step-by-step help

View step-by-step help

Exponential growth and decay: word problems

Full solution

Q. A town has a population of

17000

and grows at

3.5 \%

every year. What will be the population after

9

years, to the nearest whole number?

\newline

Answer:

Identify initial population and growth rate: Identify the initial population and the growth rate. The initial population $P_0$ is $17,000$ and the growth rate $r$ is $3.5\%$ per year.
Convert growth rate to decimal: Convert the percentage growth rate to a decimal. $\newline$ To convert a percentage to a decimal, divide by $100$ . $\newline$ $r = 3.5\% = \frac{3.5}{100} = 0.035$
Determine number of years: Determine the number of years ( $t$ ) the population will grow. $\newline$ The population will grow for $t = 9$ years.
Use exponential growth formula: Use the exponential growth formula to calculate the future population. $\newline$ The formula for exponential growth is $P(t) = P_0 \times (1 + r)^t$ . $\newline$ Substitute $P_0 = 17,000$ , $r = 0.035$ , and $t = 9$ into the formula. $\newline$ $P(9) = 17,000 \times (1 + 0.035)^9$
Calculate future population: Calculate the future population. $\newline$ $P(9) = 17,000 \times (1.035)^9$ $\newline$ First, calculate $(1.035)^9$ . $\newline$ $(1.035)^9 \approx 1.374$ $\newline$ Now, multiply this by the initial population. $\newline$ $P(9) \approx 17,000 \times 1.374$ $\newline$ $P(9) \approx 23,358$
Round to nearest whole number: Round the result to the nearest whole number. $\newline$ The population after $9$ years, rounded to the nearest whole number, is approximately $23,358$ .

More problems from Exponential growth and decay: word problems

Question

Use the following function rule to find

f(2)

\newline

f(x) = 11 \cdot (9)^x + 8

\newline

f(2) =

Posted 5 months ago

Question

Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants

400

milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of

1/3

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the amount of medication,

y

, remaining in the participant's body after

x

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

\newline

Posted 8 months ago

Question

100

bacteria doubles in size every

60

hours. What will the population be

180

?

Posted 4 months ago

Question

Charlotte opened a savings account and deposited

\$800.00

as principal. The account earns

8\%

interest, compounded annually. What is the balance after

10

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

Posted 4 months ago

Question

Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost,

f(x)

x

Posted 10 months ago

Question

Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost,

h(x)

x

Posted 10 months ago

Question

\$1,000

in a savings account with a daily interest rate of

0.1\%

. Write an exponential function to represent the total amount,

s(x)

, in his account after

x

Posted 9 months ago

Question

A=2450+740 s

\newline

The total amount,

A

, in thousands of dollars, of scholarship money given out by a college throughout its history at a time of

s

semesters after the summer of the year

2000

is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year

2000

Posted 5 months ago

Question

T=235+980 d

\newline

T

, in newton-meters, on a diving board with a

100

kilogram weight placed

d

meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?

Posted 8 months ago

Question

R=42-0.7 t

\newline

Quinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature,

R

, in degrees Celsius,

t

minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant