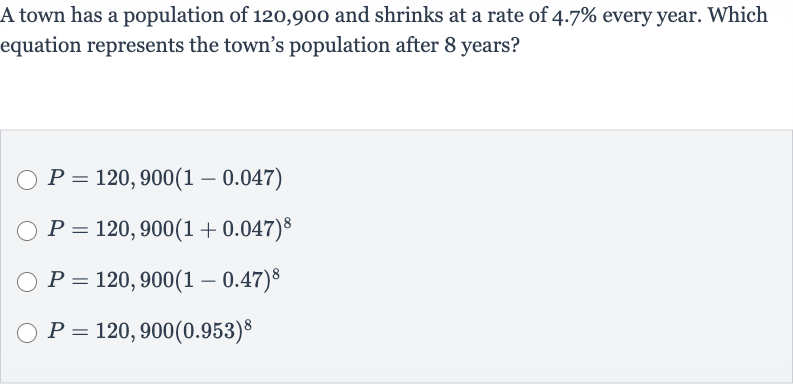Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A town has a population of 120,900 and shrinks at a rate of
4.7% every year. Which equation represents the town's population after 8 years?

P=120,900(1-0.047)

P=120,900(1+0.047)^(8)

P=120,900(1-0.47)^(8)

P=120,900(0.953)^(8)

A town has a population of $120$ , $900$ and shrinks at a rate of $4.7 \%$ every year. Which equation represents the town's population after $8$ years? $\newline$ $P=120,900(1-0.047)$ $\newline$ $P=120,900(1+0.047)^{8}$ $\newline$ $P=120,900(1-0.47)^{8}$ $\newline$ $P=120,900(0.953)^{8}$

View step-by-step help

View step-by-step help

Exponential growth and decay: word problems

Full solution

Q. A town has a population of

120

,

900

and shrinks at a rate of

4.7 \%

every year. Which equation represents the town's population after

8

years?

\newline

P=120,900(1-0.047)

\newline

P=120,900(1+0.047)^{8}

\newline

P=120,900(1-0.47)^{8}

\newline

P=120,900(0.953)^{8}

Identify initial population and rate: Identify the initial population and the annual shrinkage rate. The initial population is given as $120,900$ , and the annual shrinkage rate is $4.7\%$ .
Convert shrinkage rate to decimal: Convert the annual shrinkage rate from a percentage to a decimal. $\newline$ To convert a percentage to a decimal, divide by $100$ . $\newline$ $4.7\%$ as a decimal is $0.047$ .
Determine population decrease factor: Determine the population decrease factor for one year. $\newline$ Since the population decreases by $4.7\%$ each year, the factor by which the population decreases annually is $1 - 0.047$ .
Write equation for population after $8$ years: Write the equation that represents the population after $8$ years. $\newline$ The population after $8$ years can be found by multiplying the initial population by the decrease factor raised to the power of the number of years. $\newline$ $P = \text{initial population} \times (\text{decrease factor})^{(\text{number of years})}$ $\newline$ $P = 120,900 \times (1 - 0.047)^{8}$
Simplify decrease factor: Simplify the decrease factor. $\newline$ $1 - 0.047 = 0.953$
Substitute factor into equation: Substitute the simplified decrease factor into the equation. $\newline$ $P = 120,900 \times (0.953)^{8}$
Verify equation against options: Verify that the equation matches one of the given options. $\newline$ The correct equation is $P = 120,900 \times (0.953)^{8}$ , which matches the last option.

More problems from Exponential growth and decay: word problems

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago