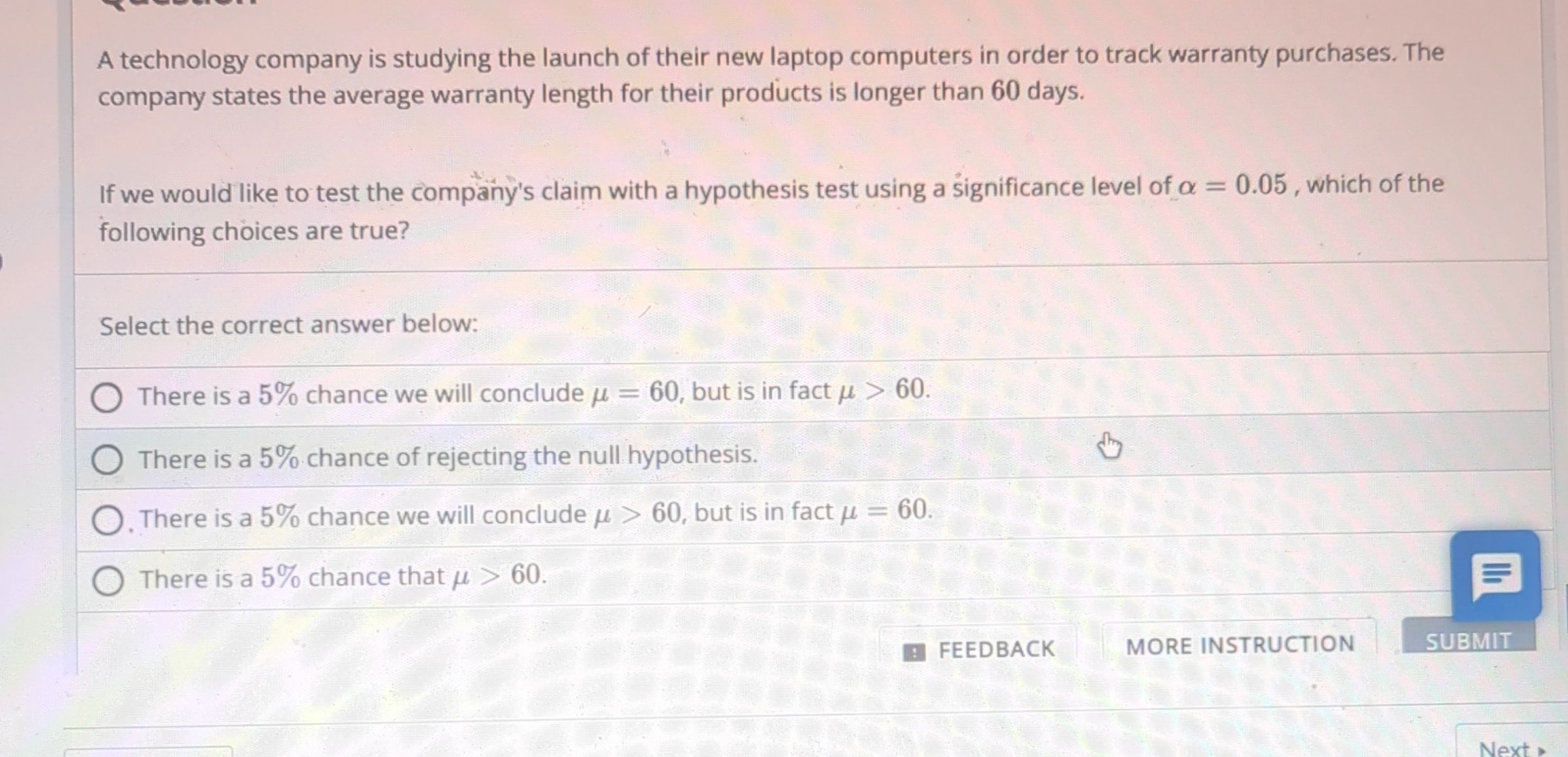
A technology company is studying the launch of their new laptop computers in order to track warranty purchases. The company states the average warranty length for their products is longer than $60$ days. $\newline$ If we would like to test the company's claim with a hypothesis test using a significance level of $\alpha=0.05$ , which of the following choices are true? $\newline$ Select the correct answer below: $\newline$ A)There is a $5 \%$ chance we will conclude $\mu=60$ , but is in fact $\mu>60$ . $\newline$ B)There is a $5 \%$ chance of rejecting the null hypothesis. $\newline$ C)There is a $5 \%$ chance we will conclude $\mu>60$ , but is in fact $\mu=60$ . $\newline$ D)There is a $5 \%$ chance that $\mu>60$ .

View step-by-step help

Home

Math Problems

Algebra 2

Find probabilities using the addition rule

Full solution

Q. A technology company is studying the launch of their new laptop computers in order to track warranty purchases. The company states the average warranty length for their products is longer than

60

days.

\newline

If we would like to test the company's claim with a hypothesis test using a significance level of

\alpha=0.05

, which of the following choices are true?

\newline

Select the correct answer below:

\newline

A)There is a

5 \%

chance we will conclude

\mu=60

, but is in fact

\mu>60

\newline

B)There is a

5 \%

chance of rejecting the null hypothesis.

\newline

C)There is a

5 \%

chance we will conclude

\mu>60

, but is in fact

\mu=60

\newline

D)There is a

5 \%

chance that

\mu>60

Define hypotheses: Define the null and alternative hypotheses for the hypothesis test. $\newline$ The null hypothesis ( $H_0$ ) is a statement that there is no effect or no difference, and it is what we assume to be true until we have evidence to suggest otherwise. In this case, the null hypothesis would be that the average warranty length is $60$ days ( $H_0: \mu = 60$ ). $\newline$ The alternative hypothesis ( $H_a$ ) is what we want to test for. It is a statement that indicates the presence of an effect or a difference. In this case, the alternative hypothesis would be that the average warranty length is greater than $60$ days ( $H_a: \mu > 60$ ).
Understand alpha: Understand the significance level (alpha). The significance level, denoted by alpha ( $\alpha$ ), is the probability of rejecting the null hypothesis when it is actually true. This is also known as the Type I error rate. In this case, alpha is set to $0.05$ , which means there is a $5\%$ risk of committing a Type I error.
Interpret significance level: Interpret the significance level in the context of the hypothesis test. The correct interpretation of the significance level in this context is that there is a $5\%$ chance of rejecting the null hypothesis (that the average warranty length is $60$ days) when it is actually true. This does not mean there is a $5\%$ chance that the average warranty length is greater than $60$ days, nor does it mean there is a $5\%$ chance that we will conclude the average warranty length is $60$ days when it is actually greater than $60$ days.
Identify correct answer: Identify the correct answer based on the interpretation of the significance level. $\newline$ The correct answer is: ＂There is a $5\%$ chance of rejecting the null hypothesis.＂ This statement correctly reflects the definition of the significance level as the probability of making a Type I error, which is rejecting the null hypothesis when it is true.