Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

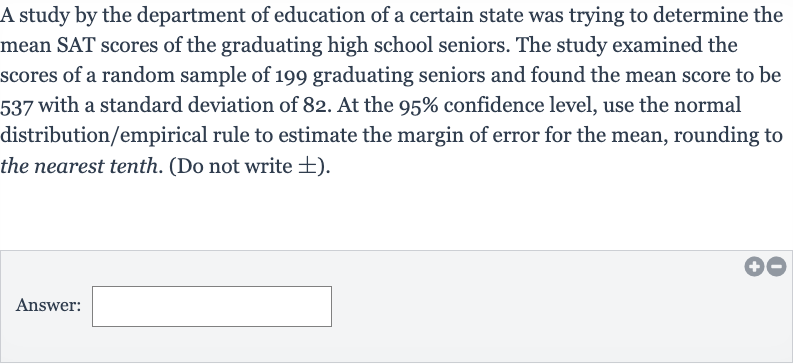
A study by the department of education of a certain state was trying to determine the mean SAT scores of the graduating high school seniors. The study examined the scores of a random sample of 199 graduating seniors and found the mean score to be 537 with a standard deviation of 82 . At the
95% confidence level, use the normal distribution/empirical rule to estimate the margin of error for the mean, rounding to the nearest tenth. (Do not write
+- ).
Answer:

A study by the department of education of a certain state was trying to determine the mean SAT scores of the graduating high school seniors. The study examined the scores of a random sample of $199$ graduating seniors and found the mean score to be $537$ with a standard deviation of $82$ . At the $95 \%$ confidence level, use the normal distribution/empirical rule to estimate the margin of error for the mean, rounding to the nearest tenth. (Do not write $\pm$ ). $\newline$ Answer:

View step-by-step help

View step-by-step help

Use normal distributions to approximate binomial distributions

Full solution

Q. A study by the department of education of a certain state was trying to determine the mean SAT scores of the graduating high school seniors. The study examined the scores of a random sample of

199

graduating seniors and found the mean score to be

537

with a standard deviation of

82

. At the

95 \%

confidence level, use the normal distribution/empirical rule to estimate the margin of error for the mean, rounding to the nearest tenth. (Do not write

\pm

).

\newline

Answer:

Identify Given Information: Identify the given information and the formula to calculate the margin of error. $\newline$ Given: $\newline$ Mean $M = 537$ $\newline$ Standard Deviation $SD = 82$ $\newline$ Sample Size $n = 199$ $\newline$ Confidence Level = $95\%$ $\newline$ The margin of error $E$ at a certain confidence level can be calculated using the formula: $\newline$ $E = Z \times (SD / \sqrt{n})$ $\newline$ Where $Z$ is the Z-score corresponding to the desired confidence level. For a $95\%$ confidence level, the Z-score is typically $1.96$ .
Calculate Margin of Error: Calculate the margin of error using the formula. $\newline$ $E = 1.96 \times (\frac{82}{\sqrt{199}})$ $\newline$ First, calculate the denominator: $\newline$ $\sqrt{199} \approx 14.1067$ $\newline$ Then, divide the standard deviation by the square root of the sample size: $\newline$ $\frac{82}{14.1067} \approx 5.8114$ $\newline$ Finally, multiply this result by the Z-score: $\newline$ $E = 1.96 \times 5.8114 \approx 11.3911$ $\newline$ Round to the nearest tenth: $\newline$ $E \approx 11.4$

More problems from Use normal distributions to approximate binomial distributions

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 1 month ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 2 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 2 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 2 months ago

Question

Y

is the number of desserts available in a randomly chosen restaurant.

\newline

Is the random variable

Y

discrete or continuous?

\newline

\newline

\text{[A]discrete}

\newline

\text{[B]continuous}

Posted 2 months ago

Question

Which of the following functions are continuous for all real numbers?

\newline

g(x)=\ln (x)

\newline

f(x)=\frac{1}{x}

\newline

1

\newline

g

\newline

f

\newline

g

f

\newline

g

f

Posted 3 months ago

Question

Which of the following functions are continuous at

x=-1

\newline

g(x)=\sin (x+1)

\newline

f(x)=\frac{1}{x-1}

\newline

1

\newline

g

\newline

f

\newline

g

f

\newline

g

f

Posted 2 months ago

Question

g

be a continuous function on the closed interval

[-1,4]

g(-1)=-4

g(4)=1

\newline

Which of the following is guaranteed by the Intermediate Value Theorem?

\newline

1

\newline

g(c)=-3

for at least one

c

-1

4

\newline

g(c)=3

for at least one

c

-4

1

\newline

g(c)=-3

for at least one

c

-4

1

\newline

g(c)=3

for at least one

c

-1

4

Posted 1 month ago