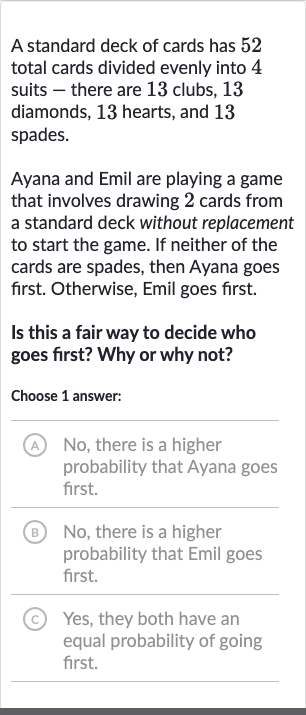
A standard deck of cards has $52$ total cards divided evenly into $4$ suits - there are $13$ clubs, $13$ diamonds, $13$ hearts, and $13$ spades. $\newline$ Ayana and Emil are playing a game that involves drawing $2$ cards from a standard deck without replacement to start the game. If neither of the cards are spades, then Ayana goes first. Otherwise, Emil goes first. $\newline$ Is this a fair way to decide who goes first? Why or why not? $\newline$ Choose $1$ answer: $\newline$ (A) No, there is a higher probability that Ayana goes first. $\newline$ (B) No, there is a higher probability that Emil goes first. $\newline$ (C) Yes, they both have an equal probability of going first.

View step-by-step help

Home

Math Problems

Algebra 2

Find probabilities using the addition rule

Full solution

Q. A standard deck of cards has

52

total cards divided evenly into

4

suits - there are

13

clubs,

13

diamonds,

13

hearts, and

13

spades.

\newline

Ayana and Emil are playing a game that involves drawing

2

cards from a standard deck without replacement to start the game. If neither of the cards are spades, then Ayana goes first. Otherwise, Emil goes first.

\newline

Is this a fair way to decide who goes first? Why or why not?

\newline

Choose

1

answer:

\newline

(A) No, there is a higher probability that Ayana goes first.

\newline

(B) No, there is a higher probability that Emil goes first.

\newline

Calculate Ayana's probability: Let's calculate the probability that Ayana goes first, which is the probability that neither of the two cards drawn are spades. $\newline$ There are $39$ non-spade cards in a standard deck of $52$ cards. The probability that the first card drawn is not a spade is $\frac{39}{52}.$
Calculate Emil's probability: Assuming the first card is not a spade, there are now $38$ non-spade cards left out of $51$ total cards. The probability that the second card drawn is also not a spade is $\frac{38}{51}.$
Compare probabilities: To find the overall probability that neither card is a spade, we multiply the probabilities of each event happening consecutively since they are independent events. $\newline$ The probability that Ayana goes first is $(39/52) \times (38/51)$ .
Conclusion: Calculating this probability gives us $(\frac{39}{52}) \times (\frac{38}{51}) = (\frac{3}{4}) \times (\frac{38}{51}) = \frac{114}{204} = \frac{57}{102}$ .
Conclusion: Calculating this probability gives us $(\frac{39}{52}) \times (\frac{38}{51}) = (\frac{3}{4}) \times (\frac{38}{51}) = \frac{114}{204} = \frac{57}{102}$ .Now let's calculate the probability that Emil goes first, which is the probability that at least one of the two cards drawn is a spade. $\newline$ The probability that Emil goes first is $1$ minus the probability that Ayana goes first, since these are the only two outcomes.
Conclusion: Calculating this probability gives us $(39/52) \times (38/51) = (3/4) \times (38/51) = 114/204 = 57/102$ .Now let's calculate the probability that Emil goes first, which is the probability that at least one of the two cards drawn is a spade. $\newline$ The probability that Emil goes first is $1$ minus the probability that Ayana goes first, since these are the only two outcomes.Subtracting the probability that Ayana goes first from $1$ gives us $1 - (57/102)$ .
Conclusion: Calculating this probability gives us $(39/52) \times (38/51) = (3/4) \times (38/51) = 114/204 = 57/102$ .Now let's calculate the probability that Emil goes first, which is the probability that at least one of the two cards drawn is a spade. $\newline$ The probability that Emil goes first is $1$ minus the probability that Ayana goes first, since these are the only two outcomes.Subtracting the probability that Ayana goes first from $1$ gives us $1 - (57/102)$ .Calculating this probability gives us $1 - (57/102) = (102/102) - (57/102) = 45/102$ .
Conclusion: Calculating this probability gives us $(39/52) \times (38/51) = (3/4) \times (38/51) = 114/204 = 57/102$ .Now let's calculate the probability that Emil goes first, which is the probability that at least one of the two cards drawn is a spade. $\newline$ The probability that Emil goes first is $1$ minus the probability that Ayana goes first, since these are the only two outcomes.Subtracting the probability that Ayana goes first from $1$ gives us $1 - (57/102)$ .Calculating this probability gives us $1 - (57/102) = (102/102) - (57/102) = 45/102$ .Comparing the probabilities, we see that the probability that Ayana goes first is $57/102$ , while the probability that Emil goes first is $45/102$ . $\newline$ Since $57/102$ is greater than $45/102$ , Ayana has a higher probability of going first.
Conclusion: Calculating this probability gives us $(39/52) \times (38/51) = (3/4) \times (38/51) = 114/204 = 57/102$ .Now let's calculate the probability that Emil goes first, which is the probability that at least one of the two cards drawn is a spade. $\newline$ The probability that Emil goes first is $1$ minus the probability that Ayana goes first, since these are the only two outcomes.Subtracting the probability that Ayana goes first from $1$ gives us $1 - (57/102)$ .Calculating this probability gives us $1 - (57/102) = (102/102) - (57/102) = 45/102$ .Comparing the probabilities, we see that the probability that Ayana goes first is $57/102$ , while the probability that Emil goes first is $45/102$ . $\newline$ Since $57/102$ is greater than $45/102$ , Ayana has a higher probability of going first.Therefore, the method of deciding who goes first is not fair because Ayana has a higher probability of going first than Emil.