AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
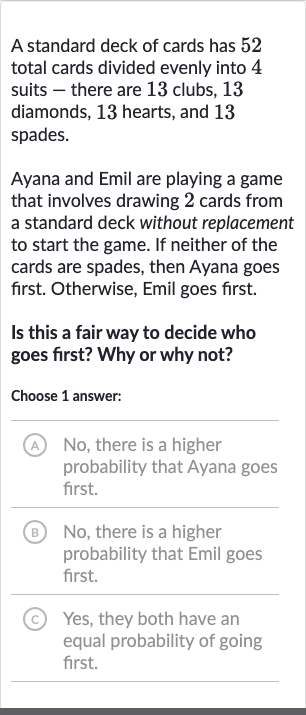
A standard deck of cards has total cards divided evenly into suits - there are clubs, diamonds, hearts, and spades.Ayana and Emil are playing a game that involves drawing cards from a standard deck without replacement to start the game. If neither of the cards are spades, then Ayana goes first. Otherwise, Emil goes first.Is this a fair way to decide who goes first? Why or why not?Choose answer:(A) No, there is a higher probability that Ayana goes first.B No, there is a higher probability that Emil goes first.(C) Yes, they both have an equal probability of going first.
Full solution
Q. A standard deck of cards has total cards divided evenly into suits - there are clubs, diamonds, hearts, and spades.Ayana and Emil are playing a game that involves drawing cards from a standard deck without replacement to start the game. If neither of the cards are spades, then Ayana goes first. Otherwise, Emil goes first.Is this a fair way to decide who goes first? Why or why not?Choose answer:(A) No, there is a higher probability that Ayana goes first.B No, there is a higher probability that Emil goes first.(C) Yes, they both have an equal probability of going first.
- Calculate Probability: Calculate the probability that neither of the two cards drawn are spades.Since there are non-spade cards in a standard deck of cards, the probability that the first card drawn is not a spade is .After drawing one non-spade card, there are non-spade cards left out of total cards. So, the probability that the second card drawn is also not a spade is .The combined probability that both cards are not spades is the product of the two probabilities:.
- Perform Calculation: Perform the calculation from Step ..This is the probability that Ayana goes first.
- Calculate Probability: Calculate the probability that at least one of the two cards drawn is a spade, which means Emil goes first.Since the probability that Ayana goes first is , the probability that Emil goes first is .
- Perform Calculation: Perform the calculation from Step ..This is the probability that Emil goes first.
- Compare Probabilities: Compare the probabilities to determine if the game is fair. If the probabilities were equal, then the game would be fair. However, the probability that Ayana goes first is higher than the probability that Emil goes first .
More problems from One-step inequalities: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
