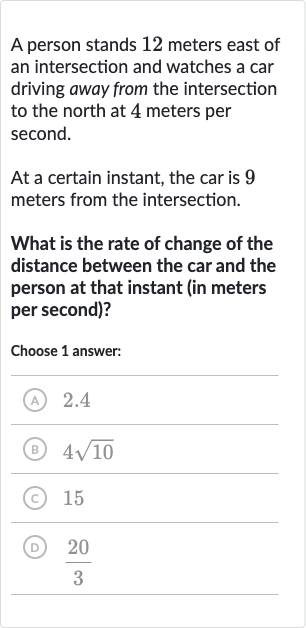
A person stands $12$ meters east of an intersection and watches a car driving away from the intersection to the north at $4$ meters per second. $\newline$ At a certain instant, the car is $9$ meters from the intersection. $\newline$ What is the rate of change of the distance between the car and the person at that instant (in meters per second)? $\newline$ Choose $1$ answer: $\newline$ (A) $2$ . $4$ $\newline$ (B) $4 \sqrt{10}$ $\newline$ (C) $15$ $\newline$ (D) $\frac{20}{3}$

Full solution

Q. A person stands

12

meters east of an intersection and watches a car driving away from the intersection to the north at

4

meters per second.

\newline

At a certain instant, the car is

9

meters from the intersection.

\newline

What is the rate of change of the distance between the car and the person at that instant (in meters per second)?

\newline

Choose

1

answer:

\newline

(A)

2

4

\newline

(B)

4 \sqrt{10}

\newline

(C)

15

\newline

(D)

\frac{20}{3}

Calculate Distance: Let's call the distance between the car and the person ＂d＂. Initially, the car is $9$ meters from the intersection and the person is $12$ meters from the intersection. Using the Pythagorean theorem, we have: $\newline$ $d^2 = 12^2 + 9^2$ $\newline$ $d^2 = 144 + 81$ $\newline$ $d^2 = 225$ $\newline$ $d = \sqrt{225}$ $\newline$ $d = 15 \text{ meters.}$
Rate of Change: Now, we need to find the rate of change of $d$ with respect to time, which is $\frac{dd}{dt}$ . Since the car is moving away from the intersection at $4$ meters per second, we can use related rates to find $\frac{dd}{dt}$ . The car's distance from the intersection is increasing, so we'll call this rate $\frac{dx}{dt} = 4 \, \text{m/s}$ .
Related Rates: Differentiating both sides of the Pythagorean equation with respect to time, we get: $\newline$ $2d\frac{dd}{dt} = 2\cdot 12\cdot(0) + 2\cdot 9\cdot\frac{dx}{dt}$ $\newline$ We know that the person is not moving, so their rate is $0$ , and $\frac{dx}{dt}$ is $4$ m/s. $\newline$ $2d\frac{dd}{dt} = 0 + 2\cdot 9\cdot 4$ $\newline$ $2d\frac{dd}{dt} = 72$
Solve for $\frac{d}{dt}$ : Now we solve for $\frac{d}{dt}$ : $\frac{d}{dt} = \frac{72}{2d}$ We already found that $d = 15$ meters, so we substitute that in: $\frac{d}{dt} = \frac{72}{2\times15}$ $\frac{d}{dt} = \frac{72}{30}$ $\frac{d}{dt} = 2.4$ meters per second.