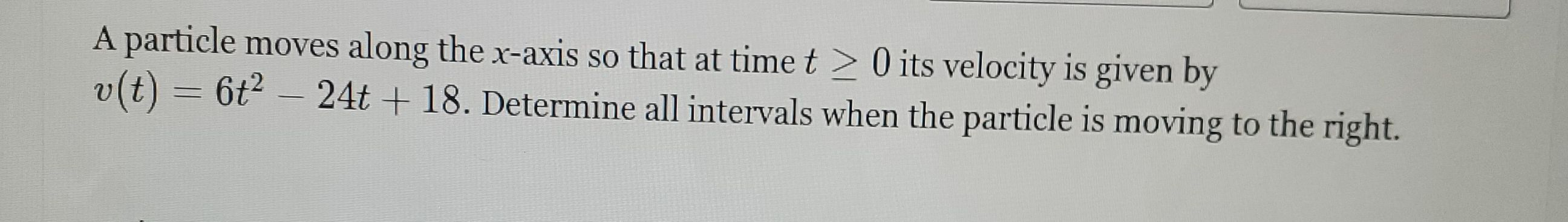A particle moves along the $x$ -axis so that at time $t \geq 0$ its velocity is given by $v(t)=6 t^{2}-24 t+18$ . Determine all intervals when the particle is moving to the right.

View step-by-step help

Home

Math Problems

Calculus

Relate position, velocity, speed, and acceleration using derivatives

Full solution

Q. A particle moves along the

x

-axis so that at time

t \geq 0

its velocity is given by

v(t)=6 t^{2}-24 t+18

. Determine all intervals when the particle is moving to the right.

Find Critical Points: To determine when the particle is moving to the right, we need to find when the velocity $v(t)$ is positive, since positive velocity indicates movement to the right on the $x$ -axis.
Factor Quadratic Equation: First, let's find the critical points of the velocity function by setting $v(t)$ equal to zero and solving for $t$ . $v(t) = 6t^2 - 24t + 18 = 0$
Test Intervals: We can factor the quadratic equation to find the roots. $\newline$ $v(t) = 6(t^2 - 4t + 3) = 6(t - 3)(t - 1) = 0$ $\newline$ So, the critical points are $t = 3$ and $t = 1$ .
Interval $(0, 1)$ : Next, we test intervals around the critical points to determine the sign of the velocity function in each interval. We choose test points in the intervals $(0, 1)$ , $(1, 3)$ , and $(3, \infty)$ .
Interval $(1, 3)$ : For the interval $(0, 1)$ , let's choose $t = 0.5$ as our test point. $\newline$ $v(0.5) = 6(0.5)^2 - 24(0.5) + 18 = 6(0.25) - 12 + 18 = 1.5 + 6 = 7.5$ $\newline$ Since v(0.5) > 0, the particle is moving to the right in the interval $(0, 1)$ .
Interval $3, \infty):</b> For the interval \$1, 3$ , let's choose $t = 2$ as our test point. $v(2) = 6(2)^2 - 24(2) + 18 = 6(4) - 48 + 18 = 24 - 48 + 18 = -6$ Since v(2) < 0, the particle is moving to the left in the interval $1, 3$ .
Combine Results: For the interval $(3, \infty)$ , let's choose $t = 4$ as our test point. $v(4) = 6(4)^2 - 24(4) + 18 = 6(16) - 96 + 18 = 96 - 96 + 18 = 18$ Since v(4) > 0, the particle is moving to the right in the interval $(3, \infty)$ .
Combine Results: For the interval $(3, \infty)$ , let's choose $t = 4$ as our test point. $v(4) = 6(4)^2 - 24(4) + 18 = 6(16) - 96 + 18 = 96 - 96 + 18 = 18$ Since v(4) > 0, the particle is moving to the right in the interval $(3, \infty)$ .Combining our results, the particle is moving to the right on the intervals $(0, 1)$ and $(3, \infty)$ .

More problems from Relate position, velocity, speed, and acceleration using derivatives

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=t^{0.7} \sin (2 t+3)$ . What is the acceleration of the particle at time $t=4$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=t^{1.1} \cos \left(t^{2}-5\right)$ . If the position of the particle is $x=-2$ when $t=2.5$ , what is the position of the particle when $t=1$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=t^{0.9} \sin (t-1)$ . If the position of the particle is $x=-3$ when $t=3$ , what is the position of the particle when $t=5$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=t^{2.1} \sin (2 t)$ . Find all times when the speed of the particle is equal to $2$ on the interval $0 \leq t \leq 4$ . You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer: $t=$
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=\left(t^{2.3}+5\right) \sin (2 t)$ . What is the distance traveled by the particle over the interval $0 \leq t \leq 5$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=t^{1.9} \cos (3 t-1)$ . What is the distance traveled by the particle over the interval $0 \leq t \leq 3$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=\left(t^{1.6}+3\right) \cos (3 t)$ . What is the average velocity of the particle on the interval $0 \leq t \leq 6$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its acceleration is given by $a(t)=\left(t^{0.5}+3\right) \cos (3 t)$ . If the velocity of the particle is $v=-2$ when $t=1$ , what is the velocity of the particle when $t=1$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=t^{2.1} \sin (2 t+5)$ . Find all times when the speed of the particle is equal to $1$ on the interval $0 \leq t \leq 3$ . You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer: $t=$
Get tutor help
Posted 9 months ago

Question
A particle travels along the $x$ -axis such that its velocity is given by $v(t)=\left(t^{2.1}+5\right) \cos (2 t)$ . What is the distance traveled by the particle over the interval $0 \leq t \leq 5$ ? You may use a calculator and round your answer to the nearest thousandth. $\newline$ Answer:
Get tutor help
Posted 9 months ago

View all (107)

A particle moves along the x x x-axis so that at time t≥0 t \geq 0 t≥0 its velocity is given by v(t)=6t2−24t+18 v(t)=6 t^{2}-24 t+18 v(t)=6t2−24t+18. Determine all intervals when the particle is moving to the right.

A particle moves along the $x$ -axis so that at time $t \geq 0$ its velocity is given by $v(t)=6 t^{2}-24 t+18$ . Determine all intervals when the particle is moving to the right.