Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A particle moves along the
x-axis so that at time
t >= 0 its velocity is given by
v(t)=3t^(2)+12 t-36. Determine all values of
t when the particle is at rest.
Answer:
t=

A particle moves along the $x$ -axis so that at time $t \geq 0$ its velocity is given by $v(t)=3 t^{2}+12 t-36$ . Determine all values of $t$ when the particle is at rest. $\newline$ Answer: $t=$

View step-by-step help

View step-by-step help

Relate position, velocity, speed, and acceleration using derivatives

Full solution

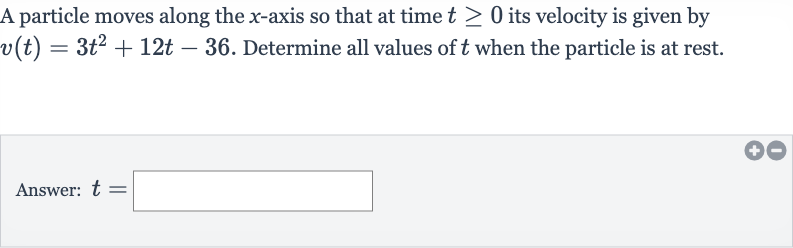
Q. A particle moves along the

x

-axis so that at time

t \geq 0

its velocity is given by

v(t)=3 t^{2}+12 t-36

. Determine all values of

t

when the particle is at rest.

\newline

Answer:

t=

Set Velocity Function Equal: To find when the particle is at rest, we need to set the velocity function $v(t)$ equal to zero and solve for $t$ . $v(t) = 3t^2 + 12t - 36$ $0 = 3t^2 + 12t - 36$
Simplify by Dividing: We can simplify the equation by dividing all terms by $3$ , which is the greatest common divisor of the coefficients. $\newline$ $0 = t^2 + 4t - 12$
Factor Quadratic Equation: Now we need to factor the quadratic equation $t^2 + 4t - 12$ . $(t + 6)(t - 2) = 0$
Solve for Values of t: Setting each factor equal to zero gives us the values of t when the particle is at rest. $\newline$ $t + 6 = 0$ or $t - 2 = 0$
Consider Domain: Solving each equation for $t$ gives us the two values when the particle is at rest. $t = -6$ or $t = 2$
Final Value of t: However, we must consider the domain of the problem, which is $t \geq 0$ . Since $t = -6$ is not within the domain, we discard it. $\newline$ The only value of $t$ when the particle is at rest is $t = 2$ .

More problems from Relate position, velocity, speed, and acceleration using derivatives

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=t^{0.7} \sin (2 t+3)

. What is the acceleration of the particle at time

t=4

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=t^{1.1} \cos \left(t^{2}-5\right)

. If the position of the particle is

x=-2

t=2.5

, what is the position of the particle when

t=1

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=t^{0.9} \sin (t-1)

. If the position of the particle is

x=-3

t=3

, what is the position of the particle when

t=5

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=t^{2.1} \sin (2 t)

. Find all times when the speed of the particle is equal to

2

on the interval

0 \leq t \leq 4

. You may use a calculator and round your answer to the nearest thousandth.

\newline

t=

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=\left(t^{2.3}+5\right) \sin (2 t)

. What is the distance traveled by the particle over the interval

0 \leq t \leq 5

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=t^{1.9} \cos (3 t-1)

. What is the distance traveled by the particle over the interval

0 \leq t \leq 3

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=\left(t^{1.6}+3\right) \cos (3 t)

. What is the average velocity of the particle on the interval

0 \leq t \leq 6

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its acceleration is given by

a(t)=\left(t^{0.5}+3\right) \cos (3 t)

. If the velocity of the particle is

v=-2

t=1

, what is the velocity of the particle when

t=1

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=t^{2.1} \sin (2 t+5)

. Find all times when the speed of the particle is equal to

1

on the interval

0 \leq t \leq 3

. You may use a calculator and round your answer to the nearest thousandth.

\newline

t=

Posted 9 months ago

Question

A particle travels along the

x

-axis such that its velocity is given by

v(t)=\left(t^{2.1}+5\right) \cos (2 t)

. What is the distance traveled by the particle over the interval

0 \leq t \leq 5

? You may use a calculator and round your answer to the nearest thousandth.

\newline

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant