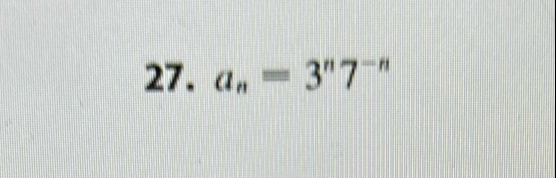Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify a_(n)=3^(n)7^(-n)

Simplify. an=3n7−n a_{n}=3^{n} 7^{-n}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Add, subtract, multiply, and divide polynomialsright chevron icon

Full solution

Q. Simplify. an=3n7−n a_{n}=3^{n} 7^{-n}
  1. Identify Expression: Identify the expression to be simplified.\newlineWe are given the expression an=3n7−na_{n}=3^{n}7^{-n} and need to simplify it.
  2. Apply Exponent Laws: Apply the laws of exponents to simplify the expression.\newlineSince the expression involves powers of 33 and 77 with the same exponent but different bases, we can combine them by division as per the laws of exponents.\newlinean=3n7na_{n} = \frac{3^{n}}{7^{n}}
  3. Rewrite as Single Power: Rewrite the expression as a single power with the base of the fraction.\newlineUsing the property that am/bm=(a/b)ma^{m}/b^{m} = (a/b)^{m}, we can rewrite the expression as:\newlinean=(37)na_{n} = (\frac{3}{7})^{n}

More problems from Add, subtract, multiply, and divide polynomials

Question
Find the degree of this polynomial.\newline`5b^{10} + 3b^3`\newline_______
Get tutor helpright-arrow

Posted 5 months ago

Question
Subtract.\newline(9a+5)−(2a+4)(9a + 5) - (2a + 4)\newline____
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the product. Simplify your answer. \newline−3v2(v2−9)-3v^2(v^2 - 9)\newline________
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the product. Simplify your answer.\newline(v−3)(4v+1)(v - 3)(4v + 1)\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the square. Simplify your answer.\newline(3y+2)2(3y + 2)^2\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Divide. If there is a remainder, include it as a simplified fraction.\newline(24t2+36t)÷6t(24t^2 + 36t) \div 6t\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Is the function q(x)=x6−9 q(x) = x^6 - 9 even, odd, or neither?\newlineChoices:\newline[[even][odd][neither]]\text{[[even][odd][neither]]}
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the product. Simplify your answer. \newline−3q2(−3q2+q)-3q^2(-3q^2 + q)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the product. Simplify your answer.\newline(r+3)(4r+2)(r + 3)(4r + 2)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the roots of the factored polynomial.\newline(x+7)(x+4)(x + 7)(x + 4)\newlineWrite your answer as a list of values separated by commas.\newlinex=x = ____
Get tutor helpright-arrow

Posted 9 months ago

View all (244)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant