Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

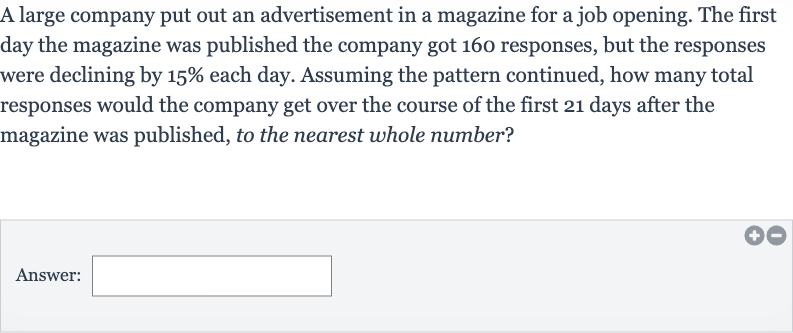
A large company put out an advertisement in a magazine for a job opening. The first day the magazine was published the company got 160 responses, but the responses were declining by 15% each day. Assuming the pattern continued, how many total responses would the company get over the course of the first 21 days after the magazine was published, to the nearest whole number? Answer:

A large company put out an advertisement in a magazine for a job opening. The first day the magazine was published the company got 160160 responses, but the responses were declining by 15% 15 \% each day. Assuming the pattern continued, how many total responses would the company get over the course of the first 2121 days after the magazine was published, to the nearest whole number?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Find probabilities using the binomial distributionright chevron icon

Full solution

Q. A large company put out an advertisement in a magazine for a job opening. The first day the magazine was published the company got 160160 responses, but the responses were declining by 15% 15 \% each day. Assuming the pattern continued, how many total responses would the company get over the course of the first 2121 days after the magazine was published, to the nearest whole number?\newlineAnswer:
  1. Identify Initial Data: Identify the initial number of responses and the daily decline rate.\newlineInitial responses on the first day: 160160\newlineDaily decline rate: 15%15\%\newlineWe need to calculate the total number of responses over 2121 days, considering a 15%15\% decline each day.
  2. Calculate Daily Responses: Calculate the number of responses for each day using the formula for a geometric sequence.\newlineThe number of responses on the nnth day can be calculated using the formula:\newlineResponsesn=Initial responses×(1−decline rate)(n−1)\text{Responses}_n = \text{Initial responses} \times (1 - \text{decline rate})^{(n-1)}\newlineWhere decline rate is 0.150.15 (15%15\% as a decimal).
  3. Calculate Total Responses: Calculate the total number of responses over 2121 days.\newlineWe will sum up the responses for each day using the formula from Step 22.\newlineTotal responses =Responsesday1+Responsesday2+…+Responsesday21= \text{Responses}_{\text{day}1} + \text{Responses}_{\text{day}2} + \ldots + \text{Responses}_{\text{day}21}\newlineWe will use a loop or a summation formula to calculate this total.
  4. Perform Daily Calculations: Perform the calculations for each day and sum them up.\newlineLet's start by calculating the first few terms to ensure our formula is correct.\newlineResponsesday1_{\text{day1}} = 160×(1−0.15)(1−1)=160×1=160160 \times (1 - 0.15)^{(1-1)} = 160 \times 1 = 160\newlineResponsesday2_{\text{day2}} = 160×(1−0.15)(2−1)=160×0.85=136160 \times (1 - 0.15)^{(2-1)} = 160 \times 0.85 = 136\newlineResponsesday3_{\text{day3}} = 160×(1−0.15)(3−1)=160×0.852≈115.6160 \times (1 - 0.15)^{(3-1)} = 160 \times 0.85^2 \approx 115.6\newline...\newlineWe will continue this process until we reach day 2121.
  5. Use Calculator for Sum: Use a calculator or a software tool to sum the geometric series.\newlineSince manually calculating each term and summing them up is time-consuming and prone to error, we will use a calculator or software to find the sum of the geometric series from day 11 to day 2121.
  6. Calculate Geometric Series Sum: Calculate the sum of the geometric series.\newlineThe sum of a geometric series can be calculated using the formula:\newlineSum = a×(1−rn)/(1−r)a \times (1 - r^n) / (1 - r)\newlineWhere:\newlinea = first term of the series (160160 responses)\newliner = common ratio (0.850.85, since the decline is 15\%))\(\newlinen = number of terms (\$21\) days)\(\newline\)Sum = \(160 \times (1 - 0.85^{21}) / (1 - 0.85)\)
  7. Evaluate Total Responses: Evaluate the sum to the nearest whole number.\(\newline\)Using the formula from Step \(6\), we calculate the sum.\(\newline\)Sum \(\approx 160 \times (1 - 0.85^{21}) / (1 - 0.85)\)\(\newline\)Sum \(\approx 160 \times (1 - 0.08589) / 0.15\)\(\newline\)Sum \(\approx 160 \times 0.91411 / 0.15\)\(\newline\)Sum \(\approx 975.05\)\(\newline\)Rounded to the nearest whole number, the total number of responses is approximately \(975\).

More problems from Find probabilities using the binomial distribution

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 9 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 9 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 9 months ago

Question
Y Y is the number of desserts available in a randomly chosen restaurant.\newlineIs the random variable Y Y discrete or continuous?\newlineChoices:\newline[A]discrete \text{[A]discrete} \newline[B]continuous \text{[B]continuous}
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous for all real numbers?\newlineg(x)=ln⁡(x) g(x)=\ln (x) \newlinef(x)=1x f(x)=\frac{1}{x} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newlineD Neither g g nor f f
Get tutor helpright-arrow

Posted 9 months ago

Question
Which of the following functions are continuous at x=−1 x=-1 ?\newlineg(x)=sin⁡(x+1) g(x)=\sin (x+1) \newlinef(x)=1x−1 f(x)=\frac{1}{x-1} \newlineChoose 11 answer:\newline(A) g g only\newline(B) f f only\newline(C) Both g g and f f \newline(D) Neither g g nor f f
Get tutor helpright-arrow

Posted 8 months ago

Question
Let g g be a continuous function on the closed interval [−1,4] [-1,4] , where g(−1)=−4 g(-1)=-4 and g(4)=1 g(4)=1 .\newlineWhich of the following is guaranteed by the Intermediate Value Theorem?\newlineChoose 11 answer:\newline(A) g(c)=−3 g(c)=-3 for at least one c c between −1-1 and 44\newline(B) g(c)=3 g(c)=3 for at least one c c between −4-4 and 11\newline(C) g(c)=−3 g(c)=-3 for at least one c c between −4-4 and 11\newline(D) g(c)=3 g(c)=3 for at least one c c between −1-1 and 44
Get tutor helpright-arrow

Posted 8 months ago

View all (89)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant