AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
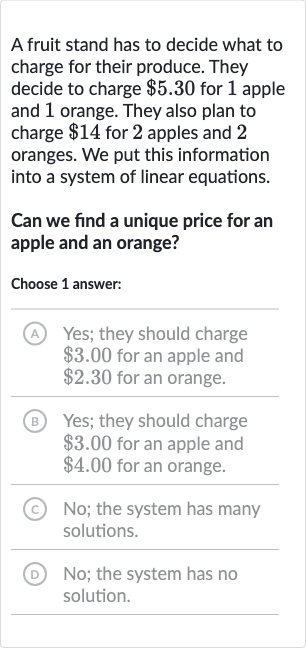
A fruit stand has to decide what to charge for their produce. They decide to charge for apple and orange. They also plan to charge for apples and oranges. We put this information into a system of linear equations.Can we find a unique price for an apple and an orange?Choose answer:(A) Yes; they should charge for an apple and for an orange.(B) Yes; they should charge for an apple and for an orange.(C) No; the system has many solutions.(D) No; the system has no solution.
Full solution
Q. A fruit stand has to decide what to charge for their produce. They decide to charge for apple and orange. They also plan to charge for apples and oranges. We put this information into a system of linear equations.Can we find a unique price for an apple and an orange?Choose answer:(A) Yes; they should charge for an apple and for an orange.(B) Yes; they should charge for an apple and for an orange.(C) No; the system has many solutions.(D) No; the system has no solution.
- Equations Setup: Let's denote the price of an apple as and the price of an orange as . We can then write two equations based on the information given:. For apple and orange, the cost is : . For apples and oranges, the cost is :
- Simplifying Equations: We can simplify the second equation by dividing each term by to make it easier to compare with the first equation:Now we have two equations:. .
- Comparison of Equations: By comparing the two equations, we can see that they cannot both be true at the same time because they give different sums for the same combination of one apple and one orange. This means that there is no unique solution to this system of equations.
More problems from Experimental probability
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
