Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

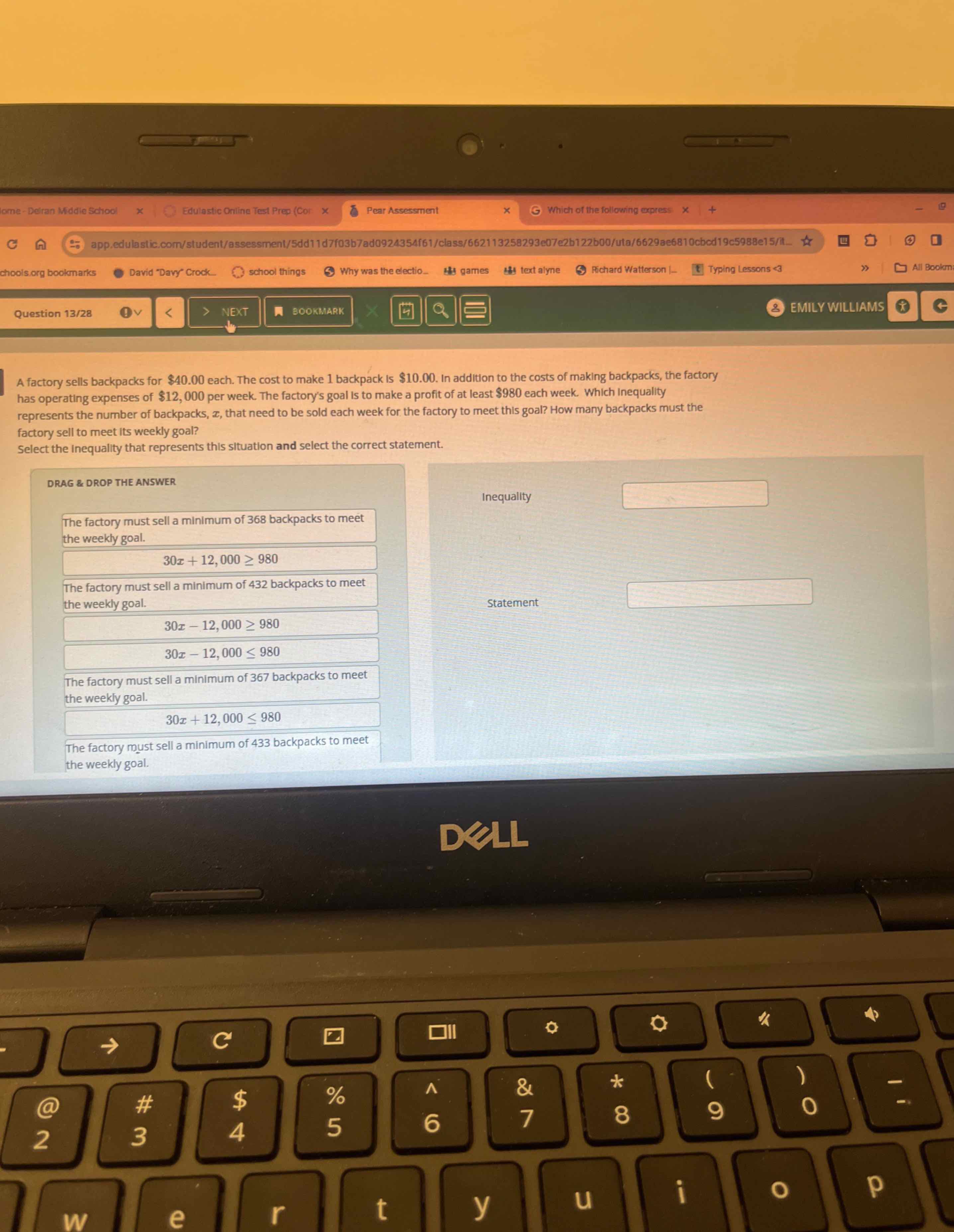
A factory sells backpacks for $40.00 each. The cost to make 1 backpack is $10.00. In addition to the costs of making backpacks, the factory has operating expenses of $12,000 per week. The factory's goal is to make a profit of at least $980 each week. Which inequality represents the number of backpacks, x, that need to be sold each week for the factory to meet thls goal? How many backpacks must the factory sell to meet its weekly goal? Select the inequality that represents this situation and select the correct statement. DRAG & DROP THE ANSWER Inequality EMILY WILLIAMS Question 13/28 NEXT BOOKMARK Which of the following express app.edulastic.com/student/assessment/5dd11d7f03b7ad0924354f61/class/662113258293e07e2b122b00/uta/6629ae6810cbod19c5988e15/t chools org booknarks David "Davy" Crock school things Why was the efectio- games text alyne Pfichard Watterson : Typing Lessons 3 All Bookm (8) EMILY WILLIAMS ( G

A factory sells backpacks for $40.00\$40.00 each. The cost to make 11 backpack is $10.00\$10.00. In addition to the costs of making backpacks, the factory has operating expenses of $12,000\$12,000 per week. The factory's goal is to make a profit of at least $980\$980 each week. Which inequality represents the number of backpacks, xx, that need to be sold each week for the factory to meet thls goal? How many backpacks must the factory sell to meet its weekly goal? Select the inequality that represents this situation and select the correct statement. DRAG & DROP THE ANSWER Inequality EMILY WILLIAMS Question 1313/2828 NEXT BOOKMARK Which of the following express app.edulastic.com/student/assessment/55dd1111d77f0303b77ad09243540924354f6161/class/662113258293662113258293e0707e22b122122b0000/uta/66296629ae68106810cbod1919c59885988e1515/t chools org booknarks David ＂Davy＂ Crock school things Why was the efectio- games text alyne Pfichard Watterson : Typing Lessons 33 All Bookm (88) EMILY WILLIAMS (

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 6right chevron icon
One-step inequalities: word problemsright chevron icon

Full solution

Q. A factory sells backpacks for $40.00\$40.00 each. The cost to make 11 backpack is $10.00\$10.00. In addition to the costs of making backpacks, the factory has operating expenses of $12,000\$12,000 per week. The factory's goal is to make a profit of at least $980\$980 each week. Which inequality represents the number of backpacks, xx, that need to be sold each week for the factory to meet thls goal? How many backpacks must the factory sell to meet its weekly goal? Select the inequality that represents this situation and select the correct statement. DRAG & DROP THE ANSWER Inequality EMILY WILLIAMS Question 1313/2828 NEXT BOOKMARK Which of the following express app.edulastic.com/student/assessment/55dd1111d77f0303b77ad09243540924354f6161/class/662113258293662113258293e0707e22b122122b0000/uta/66296629ae68106810cbod1919c59885988e1515/t chools org booknarks David ＂Davy＂ Crock school things Why was the efectio- games text alyne Pfichard Watterson : Typing Lessons 33 All Bookm (88) EMILY WILLIAMS (
  1. Calculate Profit Per Backpack: Calculate the profit per backpack sold. Subtract the cost of making one backpack from the selling price.
  2. Set Up Inequality: Set up the inequality to find the minimum number of backpacks, xx, needed to cover the operating expenses and achieve the weekly profit goal.
  3. Solve for xx: Solve the inequality for xx.
  4. Isolate xx: Divide both sides by 3030 to isolate xx.
  5. Round Up to Nearest Whole Number: Since xx represents the number of backpacks, and it cannot be a fraction, round up to the nearest whole number.

More problems from One-step inequalities: word problems

Question
−11x≥−33 -11 x \geq-33 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) x≤−3 x \leq-3 \newline(B) x≥−3 x \geq-3 \newline(C) x≤3 x \leq 3 \newline(D) x≥3 x \geq 3
Get tutor helpright-arrow

Posted 3 months ago

Question
32q≤92q−18 \frac{3}{2} q \leq \frac{9}{2} q-18 \newlineWhich of the following best describes the solutions to the inequality shown?\newlineChoose 11 answer:\newline(A) q≤3 q \leq 3 \newline(B) q≥3 q \geq 3 \newline(C) q≤6 q \leq 6 \newline(D) q≥6 q \geq 6
Get tutor helpright-arrow

Posted 3 months ago

Question
Let g(x)=5−ex g(x)=5-e^{x} .\newlineBelow is Sean's attempt to write a formal justification for the fact that the equation g(x)=0 g(x)=0 has a solution where 1≤x≤4 1 \leq x \leq 4 .\newlineIs Sean's justification complete? If not, why?\newlineSean's justification:\newlineg g is defined for all real numbers, and exponential functions are continuous at all points in their domains.\newlineSo, according to the intermediate value theorem, g(x)=0 g(x)=0 must have a solution somewhere between x=1 x=1 and x=4 x=4 .\newlineChoose 11 answer:\newline(A) Yes, Sean's justification is complete.\newline(B) No, Sean didn't establish that 00 is between g(1) g(1) and g(4) g(4) .\newline(C) No, Sean didn't establish that g g is continuous.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let f(x)=cos⁡(π⋅x)3 f(x)=\sqrt[3]{\cos (\pi \cdot x)} .\newlineBelow is Issac's attempt to write a formal justification for the fact that the equation f(x)=0.1 f(x)=0.1 has a solution where 1.5≤x≤2 1.5 \leq x \leq 2 .\newlineIs Issac's justification complete? If not, why?\newlineIssac's justification:\newlinef(1.5)=0 and f(2)=1, so f(1.5)<0.1<f(2). \begin{array}{l} f(1.5)=0 \text { and } \\ f(2)=1 \text {, so } \\ f(1.5)<0.1<f(2) . \end{array} \newlineSo, according to the intermediate value theorem, f(x)=0.1 f(x)=0.1 must have a solution when x x is between x=1.5 x=1.5 and x=2 x=2 .\newlineChoose 11 answer:\newline(A) Yes, Issac's justification is complete.\newline(B) No, Issac didn't establish that 00.11 is between f(1.5) f(1.5) and f(2) f(2) .\newline(C) No, Issac didn't establish that f f is continuous.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let h(x)=5⋅tan⁡(x) h(x)=5 \cdot \tan (x) .\newlineBelow is Bridget's attempt to write a formal justification for the fact that the equation h(x)=2 h(x)=2 has a solution where 0≤x≤π4 0 \leq x \leq \frac{\pi}{4} .\newlineIs Bridget's justification complete? If not, why?\newlineBridget's justification:\newlineh h is defined over the entire interval [0,π4] \left[0, \frac{\pi}{4}\right] , and trigonometric functions are continuous at all points in their domains.\newlineSo, according to the intermediate value theorem, h(x)=2 h(x)=2 must have a solution at some point in that interval.\newlineChoose 11 answer:\newline(A) Yes, Bridget's justification is complete.\newline(B) No, Bridget didn't establish that 22 is between h(0) h(0) and h(π4) h\left(\frac{\pi}{4}\right) .\newline(C) No, Bridget didn't establish that h h is continuous.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let f(x)=25−2x f(x)=2^{5-2 x} .\newlineBelow is Ibrahim's attempt to write a formal justification for the fact that the equation f(x)=10 f(x)=10 has a solution where −1≤x≤4 -1 \leq x \leq 4 .\newlineIs Ibrahim's justification complete? If not, why?\newlineIbrahim's justification:\newlinef f is defined for all real numbers, and exponential functions are continuous at all points in their domains. Also, f(−1)=128 f(-1)=128 and f(4)=18 f(4)=\frac{1}{8} , so 1010 is between f(−1) f(-1) and f(4) f(4) .\newlineSo, according to the intermediate value theorem, f(x)=10 f(x)=10 must have a solution at some point between x=−1 x=-1 and x=4x=4 .\newlineChoose 11 answer:\newline(A) Yes, Ibrahim's justification is complete.\newline(B) No, Ibrahim didn't establish that 1010 is between f(−1) f(-1) and f(4) f(4) .\newline(c) No, Ibrahim didn't establish that f f is continuous.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let g(x)=cos⁡(πx2) g(x)=\cos \left(\pi x^{2}\right) .\newlineBelow is Amrita's attempt to write a formal justification for the fact that the equation g′(x)=0.4 g^{\prime}(x)=0.4 has a solution where −1<x<4 -1<x<4 .\newlineIs Amrita's justification complete?\newlineIf not, why?\newlineAmrita's justification:\newlinePolynomial and trigonometric functions are differentiable and continuous at all points in their domain, and [−1,4] [-1,4] is within g′ g^{\prime} s domain. Also,\newlineg(−1)=−1 and g(4)=1, so g(4)−g(−1)4−(−1)=0.4. \begin{array}{l} g(-1)=-1 \text { and } \\ g(4)=1 \text {, so } \\ \frac{g(4)-g(-1)}{4-(-1)}=0.4 . \end{array} \newlineSo, according to the mean value theorem, g′(x)=0.4 g^{\prime}(x)=0.4 must have a solution somewhere between x=−1 x=-1 and x=4 x=4 .\newlineChoose 11 answer:\newline(A) Yes, Amrita's justification is complete.\newline(B) No, Amrita didn't establish that the average rate of change of g g over [−1,4] [-1,4] is equal to 00.44 .\newline(C) No, Amrita didn't establish that g g is differentiable.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let\newlineh(x)=x5−2x4+10x2−10x.  h(x)=x^{5}-2 x^{4}+10 x^{2}-10 x \text {. } \newlineBelow is Omar's attempt to write a formal justification for the fact that there exists a value c c where\newline−2<c<2 such that h′(c)=6.  -2<c<2 \text { such that } h^{\prime}(c)=6 \text {. } \newlineIs Omar's justification complete? If not, why?\newlineOmar's justification:\newlineh(−2)=−4 and h(2)=20, so h(2)−h(−2)2−(−2)=6. \begin{array}{l} h(-2)=-4 \text { and } \\ h(2)=20 \text {, so } \\ \frac{h(2)-h(-2)}{2-(-2)}=6 . \end{array} \newlineSo, according to the mean value theorem, there exists a value c c somewhere in the interval −2<c<2 -2<c<2 such that h′(c)=6 h^{\prime}(c)=6 .\newlineChoose 11 answer:\newline(A) Yes, Omar's justification is complete.\newline(B) No, Omar didn't establish that the average rate of change of h h over [−2,2] [-2,2] is equal to 66 .\newline(C) No, Omar didn't establish that h h is differentiable.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let f(x)=x+x3 f(x)=\sqrt{x+\sqrt{x^{3}}} .\newlineBelow is Lena's attempt to write a formal justification for the fact that the equation f′(x)=23 f^{\prime}(x)=\frac{2}{3} has a solution where 0<x<9 0<x<9 .\newlineIs Lena's justification complete? If not, why?\newlineLena's justification:\newlinef(0)=0 f(0)=0 and f(9)=6 f(9)=6 , so the average rate of change of f f over the interval 0≤x≤9 0 \leq x \leq 9 is 23 \frac{2}{3} .\newlineSo, according to the mean value theorem, f′(x)=23 f^{\prime}(x)=\frac{2}{3} must have a solution somewhere in the interval 0<x<9 0<x<9 .\newlineChoose 11 answer:\newline(A) Yes, Lena's justification is complete.\newline(B) No, Lena didn't establish that the average rate of change of f f over[0,9] [0,9] is equal to 23 \frac{2}{3} .\newline(C) No, Lena didn't establish that f f is differentiable.
Get tutor helpright-arrow

Posted 3 months ago

Question
Let h(x)=3x−x2 h(x)=3^{x}-x^{2} .\newlineBelow is Uriah's attempt to write a formal justification for the fact that the equation h′(x)=8 h^{\prime}(x)=8 has a solution where 1<x<3 1<x<3 .\newlineIs Uriah's justification complete? If not, why?\newlineUriah's justification:\newlinePolynomial and exponential functions are differentiable and continuous at all points in their domain, and [1,3] [1,3] is within h h 's domain. Also, h(1)=2 h(1)=2 and h(3)=18 h(3)=18 , so\newlineh(3)−h(1)3−1=8.  \frac{h(3)-h(1)}{3-1}=8 \text {. } \newlineSo, according to the mean value theorem, h′(x)=8 h^{\prime}(x)=8 must have a solution somewhere between x=1 x=1 and x=3 x=3 .\newlineChoose 11 answer:\newline(A) Yes, Uriah's justification is complete.\newline(B) No, Uriah didn't establish that the average rate of change of h h over [1,3] [1,3] is equal to 88 .\newline(C) No, Uriah didn't establish that h h is differentiable.
Get tutor helpright-arrow

Posted 3 months ago

View all (36)