Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A cylinder has a base radius of 4 meters and a height of 2 meters. What is its volume in cubic meters, to the nearest tenths place?
Answer:
V=◻ meters
^(3)

A cylinder has a base radius of $4$ meters and a height of $2$ meters. What is its volume in cubic meters, to the nearest tenths place? $\newline$ Answer: $V=\square$ meters $^{3}$

View step-by-step help

View step-by-step help

Volume of cylinders

Full solution

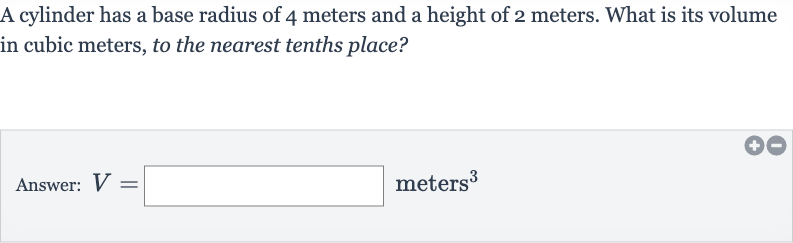
Q. A cylinder has a base radius of

4

meters and a height of

2

meters. What is its volume in cubic meters, to the nearest tenths place?

\newline

Answer:

V=\square

meters

^{3}

Identify Formula and Values: Identify the formula for the volume of a cylinder and the given values. $\newline$ The formula for the volume of a cylinder is $V = \pi r^2 h$ , where $V$ is the volume, $r$ is the radius of the base, and $h$ is the height of the cylinder. $\newline$ Given values: $\newline$ Radius ( $r$ ): $4$ m $\newline$ Height ( $h$ ): $2$ m
Plug Given Values: Plug the given values into the formula to calculate the volume. $\newline$ Using the given values, the volume $V$ is calculated as follows: $\newline$ $V = \pi \times (4 \, \text{m})^2 \times (2 \, \text{m})$
Calculate Radius Square: Calculate the square of the radius. $\newline$ $(4 \, \text{m})^2 = 16 \, \text{m}^2$
Use Approximation of Pi: Use the approximation of $\pi$ (pi) as $3.14$ to calculate the volume. $V = 3.14 \times 16 \, \text{m}^2 \times 2 \, \text{m}$
Perform Multiplication: Perform the multiplication to find the volume. $\newline$ $V = 3.14 \times 32 \, \text{m}^3$ $\newline$ $V = 100.48 \, \text{m}^3$
Round to Nearest Tenth: Round the volume to the nearest tenth. The volume rounded to the nearest tenth is $100.5\,\text{m}^3$ .

More problems from Volume of cylinders

Question

A cylindrical soda can has a volume of

108\pi\ \text{cm}^{3}

and a height of

12\text{cm}

. What is the surface area of the soda can in square centimeters?

\newline

1

\newline

18\pi\text{cm}^{2}

\newline

36\pi\text{cm}^{2}

\newline

72\pi\text{cm}^{2}

\newline

90\pi\text{cm}^{2}

Posted 3 months ago

Question

A cake pan is in the shape of a right rectangular prism

20\,\text{cm}

20\,\text{cm}

5\,\text{cm}

high. The pan contains

1,000\,\text{cm}^3

of batter. Approximately how far is the cake batter from the top of the pan?

\newline

1

\newline

1\,\text{cm}

\newline

2.5\,\text{cm}

\newline

5\,\text{cm}

\newline

7\,\text{cm}

Posted 2 months ago

Question

A contractor is to build a new structure at a farm for seed storage. It will have a rectangular base, which is

20

35

feet long, with walls of thickness

t

feet. The structure is

90

feet tall. Excluding the volume of the walls, which of the following functions best models the volume,

V

, in cubic feet, inside the structure?

Posted 2 months ago

Question

Rocio drops a ball from a height of

4

meters. Rocio observes that each time the ball bounces, it reaches a peak height which is

\newline

79\%

of the previous peak height, as shown. Which of the following equations correctly models the ball's peak height,

\newline

h

, in meters, after

\newline

b

\newline

1

\newline

\newline

h=4\cdot0.79^{(b-1)}

\newline

\newline

h=4\cdot0.79^{b}

\newline

\newline

h=4-0.79\cdot b^{2}

\newline

\newline

h=4\cdot(1-0.79\cdot b^{2})

Posted 3 months ago

Question

Imani's grandmother's house is

5

miles west of her own house down Main Street. While at her grandmother's, Imani decides to ride her bike farther west down Main Street at

10

miles per hour. Which equation best describes the distance,

\newline

d

, in miles, Imani is from home after

\newline

t

\newline

1

\newline

d=5+10t

\newline

d=5-10t

\newline

d=5t+10

\newline

d=5t-10

Posted 2 months ago

Question

A piece of wood has a mass of

m_1

grams and a volume of

V_1

cubic centimeters. A second piece of wood has the same density

\rho

and a volume of

V_2

. What is the mass, in grams, of the second piece of wood?

Posted 3 months ago

Question

The function models

R

, the revenue, in dollars, from selling a particular board game at a price of

x

dollars. What is the revenue if the board game is sold at a price of

30

\newline

1

\newline

\$500,000

\newline

\$800,000

\newline

\$900,000

\newline

\$1,770,000

Posted 2 months ago

Question

Rocio drops a ball from a height of

4

meters. Rocio observes that each time the ball bounces, it reaches a peak height which is

79\%

of the previous peak height, as shown. Which of the following equations correctly models the ball's peak height,

h

, in meters, after

b

\newline

1

\newline

h=4\cdot0.79^{(b-1)}

\newline

h=4\cdot0.79^{b}

\newline

h=4-0.79\cdot b^{2}

\newline

h=4\cdot(1-0.79\cdot b^{2})

Posted 2 months ago

Question

What is the volume, in cubic inches, of a rectangular prism with a height of

7

inches, a width of

5

inches, and a length of

5

\newline

V=\square

^{3}

Posted 2 months ago

Question

A rectangular prism has a length of

2

inches, a height of

16

inches, and a width of

15

inches. What is its volume, in cubic inches?

\newline

V=\square

^{3}

Posted 2 months ago