Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A club is going to send 4 of its 10 members to represent the club at a conference.
How many different groups of 4 members can they send?

A club is going to send $4$ of its $10$ members to represent the club at a conference. $\newline$ How many different groups of $4$ members can they send?

View step-by-step help

View step-by-step help

Counting principle

Full solution

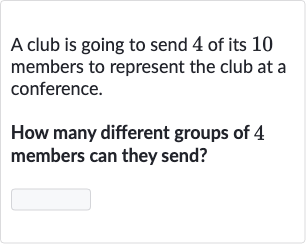
Q. A club is going to send

4

of its

10

members to represent the club at a conference.

\newline

How many different groups of

4

members can they send?

Calculate factorial of $10$ : To solve this problem, we need to calculate the number of combinations of $10$ members taken $4$ at a time. This is a combinatorial problem where order does not matter, and we can use the combination formula which is $C(n, k) = \frac{n!}{k!(n-k)!}$ , where $n$ is the total number of items, $k$ is the number of items to choose, and “ $!$ ” denotes factorial.
Calculate factorial of $4$ : First, we calculate the factorial of $10$ , which is $10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1$ .
Calculate factorial of difference: Next, we calculate the factorial of $4$ , which is $4! = 4 \times 3 \times 2 \times 1$ .
Apply combination formula: Then, we calculate the factorial of the difference between $10$ and $4$ , which is $6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1$ .
Substitute factorial values: Now we can plug these values into the combination formula: $C(10, 4) = \frac{10!}{4! \times (10-4)!}$ .
Simplify the equation: Substitute the factorial values into the formula: $C(10, 4) = \frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(4 \times 3 \times 2 \times 1) \times (6 \times 5 \times 4 \times 3 \times 2 \times 1)}$ .
Perform division and multiplication: We can simplify the equation by canceling out the common factors in the numerator and the denominator. The $6 \times 5 \times 4 \times 3 \times 2 \times 1$ in the denominator cancels with the same factors in the numerator, leaving us with: $C(10, 4) = \frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1}$ .
Final result: Perform the division and multiplication: $C(10, 4) = \frac{10 \times 9 \times 8 \times 7}{24} = 90 \times 7 = 630$ .
Final result: Perform the division and multiplication: $C(10, 4) = \frac{10 \times 9 \times 8 \times 7}{24} = 90 \times 7 = 630$ .Therefore, the club can send $630$ different groups of $4$ members to represent it at the conference.

More problems from Counting principle

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. ____ `%`

Posted 2 months ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 3 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 2 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 3 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 1 month ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 3 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 3 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 3 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 3 months ago