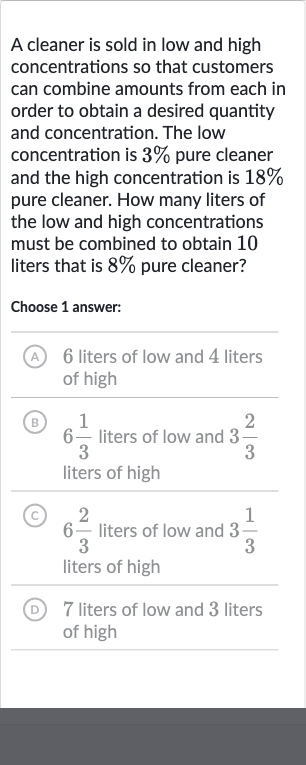
A cleaner is sold in low and high concentrations so that customers can combine amounts from each in order to obtain a desired quantity and concentration. The low concentration is $3\%$ pure cleaner and the high concentration is $18\%$ pure cleaner. How many liters of the low and high concentrations must be combined to obtain $10$ liters that is $8\%$ pure cleaner? $\newline$ Choose $1$ answer: $\newline$ (A) $6$ liters of low and $4$ liters of high $\newline$ (B) $6\frac{1}{3}$ liters of low and $3\frac{2}{3}$ liters of high $\newline$ (C) $6\frac{2}{3}$ liters of low and $3\frac{1}{3}$ liters of high $\newline$ (D) $7$ liters of low and $3$ liters of high

View step-by-step help

Home

Math Problems

Grade 7

One-step inequalities: word problems

Full solution

Q. A cleaner is sold in low and high concentrations so that customers can combine amounts from each in order to obtain a desired quantity and concentration. The low concentration is

3\%

pure cleaner and the high concentration is

18\%

pure cleaner. How many liters of the low and high concentrations must be combined to obtain

10

liters that is

8\%

pure cleaner?

\newline

Choose

1

answer:

\newline

(A)

6

liters of low and

4

liters of high

\newline

(B)

6\frac{1}{3}

liters of low and

3\frac{2}{3}

liters of high

\newline

(C)

6\frac{2}{3}

liters of low and

3\frac{1}{3}

liters of high

\newline

(D)

7

liters of low and

3

liters of high

Define Variables: Let $x$ be the amount of low concentration cleaner needed, and $y$ be the amount of high concentration cleaner needed. We know that $x + y = 10$ because we want to obtain $10$ liters in total.
Set Up Equations: We also know that the final mixture needs to be $8\%$ pure cleaner. We can set up an equation based on the concentrations: $0.03x$ ( $3\%$ of the low concentration) + $0.18y$ ( $18\%$ of the high concentration) should equal $0.08 \times 10$ ( $8\%$ of the final $10$ -liter mixture).
Solve Using Substitution: Now we have two equations: $\newline$ $1$ ) $x + y = 10$ $\newline$ $2$ ) $0.03x + 0.18y = 0.8$ $\newline$ We can solve this system of equations using substitution or elimination. Let's use substitution. From equation $1$ ), we can express $y$ as $y = 10 - x$ .
Substitute and Simplify: Substitute $y = 10 - x$ into equation $2$ ): $0.03x + 0.18(10 - x) = 0.8$ Now, distribute the $0.18$ into the parentheses: $0.03x + 1.8 - 0.18x = 0.8$ Combine like terms: $-0.15x + 1.8 = 0.8$
Isolate Variable: Subtract $1.8$ from both sides to isolate the term with $x$ : $\newline$ $-0.15x = 0.8 - 1.8$ $\newline$ $-0.15x = -1$
Find Low Concentration Amount: Divide both sides by $-0.15$ to solve for $x$ : $\newline$ $x = \frac{-1}{-0.15}$ $\newline$ $x = 6.666\ldots$ $\newline$ Since we are looking for a practical solution in terms of liters, we can round this to $x = 6\left(\frac{2}{3}\right)$ liters of low concentration cleaner.
Find High Concentration Amount: Now we can find $y$ by substituting $x$ back into $y = 10 - x$ :
$y = 10 - 6(\frac{2}{3})$
Convert $6(\frac{2}{3})$ to an improper fraction: $(6 \times 3 + 2)/3 = \frac{20}{3}$
$y = 10 - \frac{20}{3}$
$y = (\frac{30}{3}) - (\frac{20}{3})$
$y = \frac{10}{3}$
$y = 3(\frac{1}{3})$ liters of high concentration cleaner.