Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

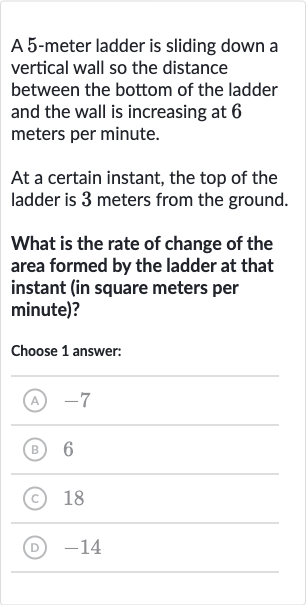
A 5-meter ladder is sliding down a vertical wall so the distance between the bottom of the ladder and the wall is increasing at 6 meters per minute.
At a certain instant, the top of the ladder is 3 meters from the ground.
What is the rate of change of the area formed by the ladder at that instant (in square meters per minute)?
Choose 1 answer:
(A) -7
(B) 6
(C) 18
(D) -14

A $5$ -meter ladder is sliding down a vertical wall so the distance between the bottom of the ladder and the wall is increasing at $6$ meters per minute. $\newline$ At a certain instant, the top of the ladder is $3$ meters from the ground. $\newline$ What is the rate of change of the area formed by the ladder at that instant (in square meters per minute)? $\newline$ Choose $1$ answer: $\newline$ (A) $-7$ $\newline$ (B) $6$ $\newline$ (C) $18$ $\newline$ (D) $-14$

View step-by-step help

View step-by-step help

Calculate unit rates with fractions

Full solution

Q. A

5

-meter ladder is sliding down a vertical wall so the distance between the bottom of the ladder and the wall is increasing at

6

meters per minute.

\newline

At a certain instant, the top of the ladder is

3

meters from the ground.

\newline

What is the rate of change of the area formed by the ladder at that instant (in square meters per minute)?

\newline

Choose

1

answer:

\newline

(A)

-7

\newline

(B)

6

\newline

(C)

18

\newline

(D)

-14

Triangle Information: The ladder, wall, and ground form a right triangle. The ladder's length is the hypotenuse, and it's $5$ meters long. The distance from the top of the ladder to the ground is $3$ meters.
Finding x: Let's call the distance from the bottom of the ladder to the wall $x$ meters. We can use the Pythagorean theorem to find $x$ . $\newline$ $5^2 = 3^2 + x^2$ $\newline$ $25 = 9 + x^2$ $\newline$ $x^2 = 25 - 9$ $\newline$ $x^2 = 16$ $\newline$ $x = 4 \text{ meters.}$
Calculating Area: The area $A$ of the triangle at that instant is $(1/2) \times \text{base} \times \text{height} = (1/2) \times x \times 3$ . $\newline$ $A = (1/2) \times 4 \times 3$ $\newline$ $A = 6$ square meters.
Rate of Change: The rate of change of $x$ is given as $6$ meters per minute. We need to find the rate of change of the area, $\frac{dA}{dt}$ . $\newline$ $\frac{dA}{dt} = \frac{1}{2} \cdot \frac{d(x \cdot 3)}{dt}$ $\newline$ $\frac{dA}{dt} = \frac{1}{2} \cdot 3 \cdot \frac{dx}{dt}$ $\newline$ $\frac{dA}{dt} = \frac{1}{2} \cdot 3 \cdot 6$ $\newline$ $\frac{dA}{dt} = 9$ square meters per minute.

More problems from Calculate unit rates with fractions

Question

What is the period of

\newline

y=\cos (-4 \pi x+3)-7 ?

\newline

Give an exact value.

\newline

Posted 4 months ago

Question

Mandy works construction. She knows that a

5

meter long metal bar has a mass of

40 \mathrm{~kg}

. Mandy wants to figure out the mass

(w)

of a bar made out of the same metal that is

3

meters long and the same thickness.

\newline

What is the mass of the shorter bar?

\newline

\mathrm{kg}

Posted 3 months ago

Question

21

6

minutes. She wants to know how many minutes

(m)

it would take her to eat

35

hot dogs if she can keep up the same pace.

\newline

How many minutes would Mika need to eat

35

\newline

Posted 3 months ago

Question

Elton is a candle maker. Each

15 \mathrm{~cm}

long candle he makes burns evenly for

6

\newline

If Elton makes a

45 \mathrm{~cm}

long candle, how long would it burn?

\newline

Posted 3 months ago

Question

Harvey the wonder hamster can run

3 \frac{1}{6} \mathrm{~km}

\frac{1}{4}

hour. Harvey runs at a constant rate.

\newline

Find his average speed in kilometers per hour.

\newline

kilometers per hour

Posted 3 months ago

Question

Aliyyah is playing a game using dice. Each player takes turns rolling and adding their roll to their score.

\newline

Aliyyah started with

-19

points and ended with

7

\newline

How many points did Aliyyah score during the game?

\newline

Posted 3 months ago

Question

A scale on a blue print drawing of a house shows that

6

centimeters represents

3

\newline

What number of centimeters on the blue print represents an actual distance of

27

\newline

Posted 3 months ago

Question

Reem is a test driver for an automobile company. The following formula gives the total distance,

d

, in feet that Reem drove a luxury car in the first

t

seconds after idling at a speed of

0

miles per hour, up to the time when she passed a particular safety cone.

\newline

d=15.69 t^{2}

\newline

Compared to the time it took Reem to pass the safety cone, how long did it take to pass a sensor that was

\frac{4}{9}

of the distance from the start?

\newline

1

\newline

\frac{16}{81}

of the time it required to pass the cone

\newline

\frac{4}{9}

of the time it required to pass the cone

\newline

\frac{2}{3}

of the time it required to pass the cone

\newline

\frac{9}{4}

of the time it required to pass the cone

Posted 3 months ago

Question

\newline

4

\newline

\newline

\newline

\newline

\newline

stera be chanchat

\newline

\newline

\newline

1

2

\newline

What is the image point of

\newline

(-6,-1)

after the transformation

\newline

R_{180}@r_{y=-x}

\newline

(1)

\newline

Posted 3 months ago

Question

An ice cream cone maker wants to build a more stable cone by increasing the diameter and decreasing the height of the cone. The cone currently has diameter

d

centimeters and height

h

, as shown. They want the height of the new cone to be

h'

. Which of the following is closest to the smallest radius the new cone can have so that the volume is at least the volume of the old cone?

Posted 3 months ago