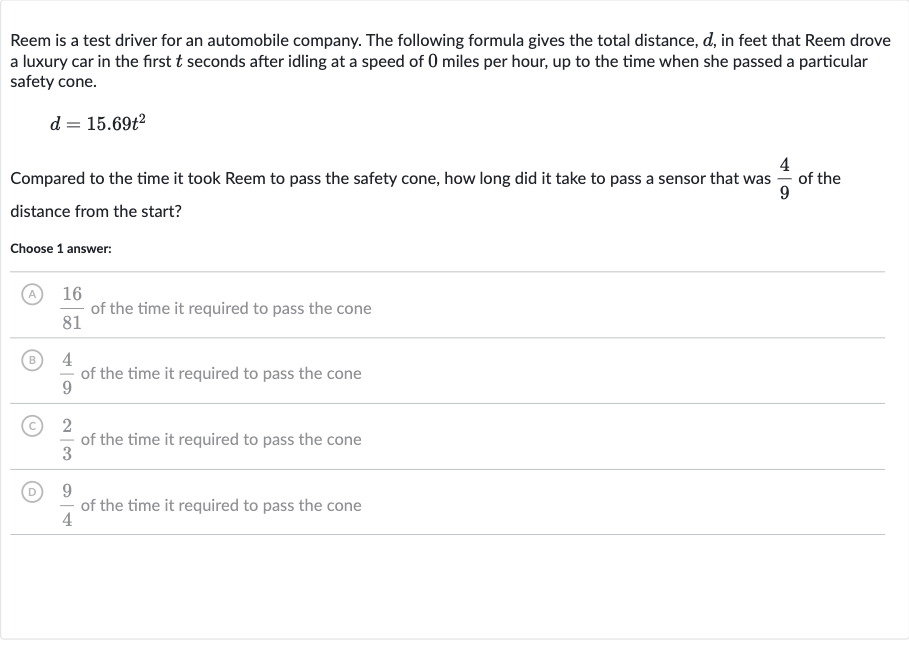
Reem is a test driver for an automobile company. The following formula gives the total distance, $d$ , in feet that Reem drove a luxury car in the first $t$ seconds after idling at a speed of $0$ miles per hour, up to the time when she passed a particular safety cone. $\newline$ $d=15.69 t^{2}$ $\newline$ Compared to the time it took Reem to pass the safety cone, how long did it take to pass a sensor that was $\frac{4}{9}$ of the distance from the start? $\newline$ Choose $1$ answer: $\newline$ A) $\frac{16}{81}$ of the time it required to pass the cone $\newline$ (B) $\frac{4}{9}$ of the time it required to pass the cone $\newline$ (C) $\frac{2}{3}$ of the time it required to pass the cone $\newline$ (D) $\frac{9}{4}$ of the time it required to pass the cone

View step-by-step help

Home

Math Problems

Grade 7

Full solution

Q. Reem is a test driver for an automobile company. The following formula gives the total distance,

d

, in feet that Reem drove a luxury car in the first

t

seconds after idling at a speed of

0

miles per hour, up to the time when she passed a particular safety cone.

\newline

d=15.69 t^{2}

\newline

Compared to the time it took Reem to pass the safety cone, how long did it take to pass a sensor that was

\frac{4}{9}

of the distance from the start?

\newline

Choose

1

answer:

\newline

\frac{16}{81}

of the time it required to pass the cone

\newline

(B)

\frac{4}{9}

of the time it required to pass the cone

\newline

(C)

\frac{2}{3}

of the time it required to pass the cone

\newline

(D)

\frac{9}{4}

of the time it required to pass the cone

Understand relationship: Understand the relationship between distance and time in the given formula. $\newline$ The formula provided is $d = 15.69t^2$ , which indicates that the distance $d$ is proportional to the square of the time $t$ . This means that if the distance changes by a factor, the time will change by the square root of that factor.
Calculate time to pass sensor: Calculate the time it takes to pass a sensor that is $(4/9)$ of the distance from the start. $\newline$ Let's denote the time it took to pass the safety cone as $T$ . The distance to the safety cone is $d = 15.69T^2$ . If the sensor is at $(4/9)$ of the distance to the cone, the distance to the sensor is $(4/9)d$ . We need to find the time it takes to reach this distance, which we'll call $t_{\text{sensor}}$ .
Set up equation: Set up the equation for the distance to the sensor. $\newline$ Using the formula $d = 15.69t^2$ , we can write the equation for the distance to the sensor as $(\frac{4}{9})d = 15.69t_{\text{sensor}}^2$ .
Substitute distance: Substitute the distance to the cone into the equation for the sensor. $\newline$ Since $d = 15.69T^2$ , we can substitute this into our equation for the sensor to get $(\frac{4}{9})(15.69T^2) = 15.69t_{\text{sensor}}^2$ .
Simplify equation: Simplify the equation to solve for $t_{\text{sensor}}$ . Divide both sides of the equation by $15.69$ to get $\left(\frac{4}{9}\right)T^2 = t_{\text{sensor}}^2$ .
Take square root: Take the square root of both sides to solve for $t_{\text{sensor}}$ . $t_{\text{sensor}} = \sqrt{\left(\frac{4}{9}\right)T^2} = \left(\sqrt{\frac{4}{9}}\right) * T = \left(\frac{2}{3}\right) * T$ .
Determine correct answer: Determine the correct answer from the given options. $\newline$ The time it took to pass the sensor is $(\frac{2}{3})$ of the time it took to pass the cone, which corresponds to answer choice (C).