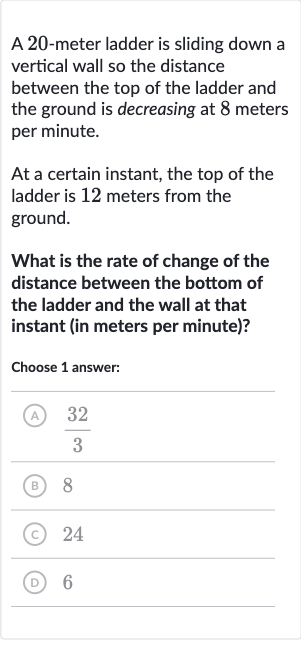
A $20$ -meter ladder is sliding down a vertical wall so the distance between the top of the ladder and the ground is decreasing at $8$ meters per minute. $\newline$ At a certain instant, the top of the ladder is $12$ meters from the ground. $\newline$ What is the rate of change of the distance between the bottom of the ladder and the wall at that instant (in meters per minute)? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{32}{3}$ $\newline$ (B) $8$ $\newline$ (C) $24$ $\newline$ (D) $6$

Full solution

Q. A

20

-meter ladder is sliding down a vertical wall so the distance between the top of the ladder and the ground is decreasing at

8

meters per minute.

\newline

At a certain instant, the top of the ladder is

12

meters from the ground.

\newline

What is the rate of change of the distance between the bottom of the ladder and the wall at that instant (in meters per minute)?

\newline

Choose

1

answer:

\newline

(A)

\frac{32}{3}

\newline

(B)

8

\newline

(C)

24

\newline

(D)

6

Triangle Description: We're dealing with a right triangle where the ladder is the hypotenuse, the distance from the wall is one leg, and the height above the ground is the other leg.
Pythagorean Theorem: Let's call the distance from the wall to the bottom of the ladder $y$ . The ladder's length is $20$ meters, and the height from the ground is $12$ meters at the instant we're considering.
Solving for x: By Pythagoras' theorem, we have $x^2 + 12^2 = 20^2$ . Let's solve for 'x'.
Rate of Change: $x^2 + 144 = 400$ $\newline$ $x^2 = 400 - 144$ $\newline$ $x^2 = 256$ $\newline$ $x = 16$ meters.
Differentiation: Now, we need to find the rate of change of $y$ with respect to time. We'll use related rates, differentiating both sides of the Pythagorean equation with respect to time $t$ .
Final Equation: Differentiating $x^2 + 12^2 = 20^2$ with respect to 't' gives us $2x(dx/dt) + 2*12*(d(12)/dt) = 0$ since the ladder's length doesn't change.
Final Equation: Differentiating $x^2 + 12^2 = 20^2$ with respect to 't' gives us $2x(dx/dt) + 2*12*(d(12)/dt) = 0$ since the ladder's length doesn't change.We know that $d(12)/dt = 0$ because the height of $12$ meters is constant at the instant we're considering. So, we have $2x(dx/dt) = 0$ .