Full solution
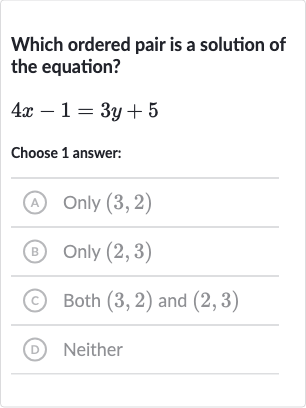
Q. Which ordered pair is a solution of the equation?Choose answer:(A) Only (B) Only (C) Both and (D) Neither
- Problem Understanding: Understand the problem.We need to determine which ordered pair satisfies the equation .
- Substituting : Substitute the and values from option (A) into the equation.For the ordered pair , substitute and into the equation and check if both sides are equal.The equation is balanced, so is a solution.
- Substituting : Substitute the and values from option (B) into the equation.For the ordered pair , substitute and into the equation and check if both sides are equal.The equation is not balanced, so is not a solution.
- Determining the Correct Answer: Determine the correct answer based on the previous steps.Since is a solution and is not, the correct answer is option (A) Only .
More problems from Does (x, y) satisfy the linear equation?
QuestionGet tutor help
QuestionGet tutor help