Full solution
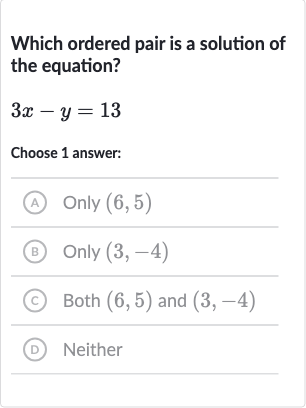
Q. Which ordered pair is a solution of the equation?Choose answer:(A) Only (B) Only (C) Both and (D) Neither
- Step : Test ordered pair : Test the ordered pair to see if it satisfies the equation .Substitute with and with into the equation: .Calculate: .Check if the result is true: .
- Step : Substitute values into equation: Since the ordered pair satisfies the equation, we can say that is a solution.
- Step : Calculate the result: Test the ordered pair to see if it satisfies the equation .Substitute with and with into the equation: .Calculate: .Check if the result is true: .
- Step : Check if the result is true: Since the ordered pair also satisfies the equation, we can say that is a solution as well.
More problems from Does (x, y) satisfy the linear equation?
QuestionGet tutor help
QuestionGet tutor help