Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following is equivalent to the complex number
i^(26) ?
Choose 1 answer:
(A) 1
(B)
i
(C) -1
(D)
-i

Which of the following is equivalent to the complex number $i^{26}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $1$ $\newline$ (B) $i$ $\newline$ (C) $-1$ $\newline$ (D) $-i$

View step-by-step help

View step-by-step help

Compare linear, exponential, and quadratic growth

Full solution

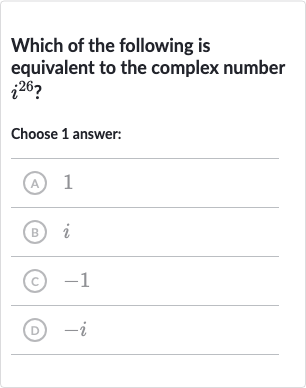
Q. Which of the following is equivalent to the complex number

i^{26}

?

\newline

Choose

1

answer:

\newline

(A)

1

\newline

(B)

i

\newline

(C)

-1

\newline

(D)

-i

Recognize the pattern: Recognize the pattern of powers of $i$ . The powers of $i$ repeat in a cycle of $4$ : $i^1 = i$ , $i^2 = -1$ , $i^3 = -i$ , $i^4 = 1$ , and then the pattern repeats.
Determine the remainder: Determine the remainder when $26$ is divided by $4$ to find where in the cycle $i^{26}$ falls. $\newline$ $26$ divided by $4$ is $6$ with a remainder of $2$ .
Use the remainder: Use the remainder to determine the equivalent power of $i$ . $\newline$ Since the remainder is $2$ , $i^{26}$ is equivalent to $i^2$ .
Calculate $i^2$ : Calculate $i^2$ . $\newline$ We know from the pattern that $i^2 = -1$ .

More problems from Compare linear, exponential, and quadratic growth

Question

We want to factor the following expression:

\newline

x^{4}+10 x+25

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

(x-2)^{4}-(y+3)^{4}

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

(x-1)^{2}+(x-1)+4

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

9 x^{4}+4 y^{2}

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

16 x^{4}-25

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

x^{4}+3 x^{2} y+9 y^{2}

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

(x+5)^{4}+2(x+5)^{2}-1

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

(x-3)^{2}-10(x-3)+25

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

(x+7)^{2}+2 y(x+7)+y^{2}

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Question

We want to factor the following expression:

\newline

9 x^{6}+6 x^{3} y+y^{2}

\newline

Which pattern can we use to factor the expression?

\newline

U

V

are either constant integers or single-variable expressions.

\newline

1

\newline

(U+V)^{2}

(U-V)^{2}

\newline

(U+V)(U-V)

\newline

(C) We can't use any of the patterns.

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant