AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
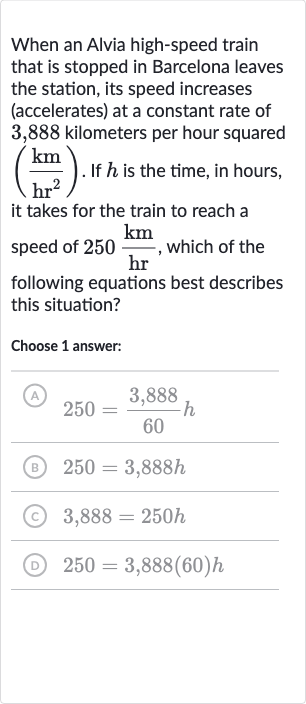
When an Alvia high-speed train that is stopped in Barcelona leaves the station, its speed increases (accelerates) at a constant rate of , kilometers per hour squared . If is the time, in hours, it takes for the train to reach a speed of , which of the following equations best describes this situation?Choose answer:(A) (B) (C) (D)
Full solution
Q. When an Alvia high-speed train that is stopped in Barcelona leaves the station, its speed increases (accelerates) at a constant rate of , kilometers per hour squared . If is the time, in hours, it takes for the train to reach a speed of , which of the following equations best describes this situation?Choose answer:(A) (B) (C) (D)
- Given Information: We are given that the train accelerates at a constant rate of . The formula for acceleration is final speed equals initial speed plus acceleration times time . Since the train starts from rest, the initial speed is . Therefore, the formula simplifies to . We need to find the time it takes for the train to reach a speed of .
- Acceleration Formula: Substitute the given values into the simplified acceleration formula. We have and . So, we get .
- Substitute Values: To find , we need to divide both sides of the equation by the acceleration . This gives us
- Calculate Time: However, we need to check the answer choices to see which one matches our equation. Choice (A) has a division by , which is not part of our calculation. Choice (B) matches our equation exactly. Choice (C) has the variables switched, and choice (D) has an unnecessary multiplication by . Therefore, the correct answer is (B) .
More problems from Write a linear inequality: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
