AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
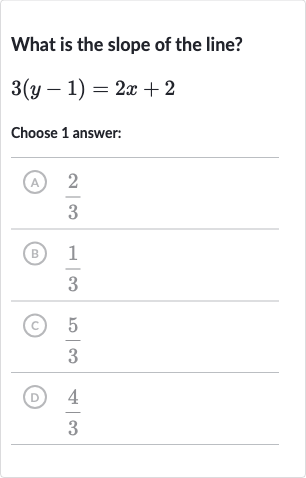
What is the slope of the line?Choose answer:(A) (B) (C) (D)
Full solution
Q. What is the slope of the line?Choose answer:(A) (B) (C) (D)
- Distribute the : Distribute the on the left side of the equation to both terms inside the parentheses.
- Rearrange to slope-intercept form: Rearrange the equation to the slope-intercept form, which is , where is the slope.First, add to both sides to isolate the y-term on one side.
- Divide all terms to solve for y: Divide all terms by to solve for .
- Identify the slope: Identify the slope from the equation .The coefficient of is the slope of the line.So, the slope .
More problems from Solve multi-step equations with fractional coefficients
QuestionGet tutor help
