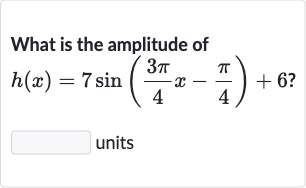Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the amplitude of

h(x)=7sin((3pi)/(4)x-(pi)/(4))+6?
units

What is the amplitude of $\newline$ $h(x)=7 \sin \left(\frac{3 \pi}{4} x-\frac{\pi}{4}\right)+6 ?$ $\newline$ units

View step-by-step help

View step-by-step help

Identify linear and exponential functions

Full solution

Q. What is the amplitude of

\newline

h(x)=7 \sin \left(\frac{3 \pi}{4} x-\frac{\pi}{4}\right)+6 ?

\newline

units

Identify Amplitude: The amplitude of a trigonometric function like $h(x)$ is the coefficient in front of the sine or cosine term, which determines the height of the peaks and the depth of the troughs from the midline of the wave. In the given function $h(x) = 7\sin\left(\frac{3\pi}{4}x - \frac{\pi}{4}\right) + 6$ , the coefficient in front of the sine term is $7$ .
Calculate Coefficient: The amplitude is always a positive value, so even if the coefficient were negative, we would take the absolute value to find the amplitude. In this case, the coefficient is already positive, so the amplitude of $h(x)$ is $7$ .

More problems from Identify linear and exponential functions

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago