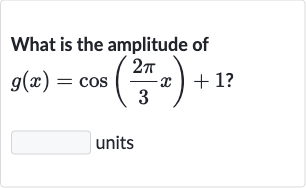Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the amplitude of

g(x)=cos((2pi)/(3)x)+1?
units

What is the amplitude of $\newline$ $g(x)=\cos \left(\frac{2 \pi}{3} x\right)+1 ?$ $\newline$ units

View step-by-step help

View step-by-step help

Identify linear and exponential functions

Full solution

Q. What is the amplitude of

\newline

g(x)=\cos \left(\frac{2 \pi}{3} x\right)+1 ?

\newline

units

Question Prompt: The question_prompt: What is the amplitude of the function $g(x) = \cos\left(\frac{2\pi}{3}x\right) + 1$ ?
Identifying Amplitude: The amplitude of a trigonometric function like cosine or sine is the coefficient in front of the cosine or sine term. In the function $g(x) = \cos\left(\frac{2\pi}{3}x\right) + 1$ , the coefficient in front of the cosine term is $1$ .
Determining Coefficient: Since there is no coefficient other than $1$ in front of the cosine term, the amplitude of the function is $1$ . The ＂ $+1$ ＂ outside of the cosine function shifts the graph vertically but does not affect the amplitude.
Final Amplitude: Therefore, the amplitude of the function $g(x) = \cos\left(\frac{2\pi}{3}x\right) + 1$ is $1$ unit.

More problems from Identify linear and exponential functions

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago