Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Vijay needs to take a taxi, which costs a flat fee of 3 dollars, plus an additional 4 dollars per mile. If Vijay has
a dollars with him, which inequality shows the number of miles,
m, he can afford to travel in the taxi?
Choose 1 answer:
(A)
0 <= m <= 4a-3
(B)
0 <= m <= (a)/(4)-(3)/(4)
(c)
4a-3 <= m
(D)
(a)/(4)-(3)/(4) <= m

Vijay needs to take a taxi, which costs a flat fee of $3$ dollars, plus an additional $4$ dollars per mile. If Vijay has $a$ dollars with him, which inequality shows the number of miles, $m$ , he can afford to travel in the taxi? $\newline$ Choose $1$ answer: $\newline$ (A) $0 \leq m \leq 4 a-3$ $\newline$ (B) $0 \leq m \leq \frac{a}{4}-\frac{3}{4}$ $\newline$ (C) $4 a-3 \leq m$ $\newline$ (D) $\frac{a}{4}-\frac{3}{4} \leq m$

View step-by-step help

View step-by-step help

Write two-variable inequalities: word problems

Full solution

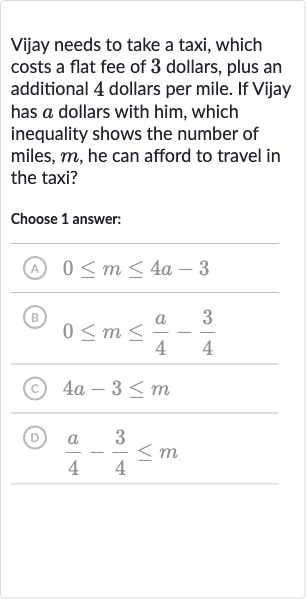
Q. Vijay needs to take a taxi, which costs a flat fee of

3

dollars, plus an additional

4

dollars per mile. If Vijay has

a

dollars with him, which inequality shows the number of miles,

m

, he can afford to travel in the taxi?

\newline

Choose

1

answer:

\newline

(A)

0 \leq m \leq 4 a-3

\newline

(B)

0 \leq m \leq \frac{a}{4}-\frac{3}{4}

\newline

(C)

4 a-3 \leq m

\newline

(D)

\frac{a}{4}-\frac{3}{4} \leq m

Calculate Total Cost: The total cost of the taxi ride for $m$ miles is the sum of the flat fee and the cost per mile. The flat fee is $3$ dollars and the cost per mile is $4$ dollars.
Represent Total Cost: The total cost for $m$ miles can be represented by the equation: $\text{Total Cost} = \text{Flat Fee} + (\text{Cost per Mile} \times \text{Number of Miles})$ .
Substitute Given Values: Substitute the given values into the equation: Total Cost $= 3 + 4m$ .
Set Up Inequality: Vijay can afford to take the taxi as long as the total cost is less than or equal to the amount of money he has, which is $a$ dollars. So, we have the inequality: $3 + 4m \leq a$ .
Isolate Variable: To find the inequality for $m$ , we need to isolate $m$ on one side. Subtract $3$ from both sides of the inequality: $4m \leq a - 3$ .
Solve for m: Now, divide both sides of the inequality by $4$ to solve for $m$ : $m \leq \frac{a - 3}{4}$ .
Rewrite Inequality: The inequality $m \leq \frac{a - 3}{4}$ can be rewritten as $0 \leq m \leq \frac{a - 3}{4}$ , since the number of miles cannot be negative.
Simplify Inequality: The inequality $0 \leq m \leq \frac{a - 3}{4}$ can be further simplified by dividing the numerator and the denominator by $4$ : $0 \leq m \leq \frac{a}{4} - \frac{3}{4}$ .

More problems from Write two-variable inequalities: word problems

Question

Write the following inequality in slope-intercept form.

\newline

9x+y \geq -17

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

\newline

Posted 5 months ago

Question

(2,\,1)

make the inequality

2x + 15y < 20

\newline

\newline

\newline

Posted 5 months ago

Question

Jack is fixing up his home and must spend less than

\$4,800

to hire carpenters and painters. Carpenters charge

\$60

per hour and painters charge

\$32

\newline

Select the inequality in standard form that describes this situation. Use the given numbers and the following variables.

\newline

x =

the number of hours of carpentry

\newline

y =

the number of hours of painting

\newline

\newline

32x + 60y < 4,800

\newline

60x + 32y < 4,800

\newline

32x - 60y < 4,800

\newline

60x - 32y < 4,800

Posted 5 months ago

Question

(2,\, 10)

a solution to this system of inequalities?

\newline

y \geq x + 10

\newline

y \leq 9x + 5

\newline

\newline

\newline

Posted 5 months ago

Question

Write the following inequality in slope-intercept form.

\newline

4x - 2y \leq 8

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Write the following inequality in slope-intercept form.

\newline

-3x + 5y > 15

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Write the following inequality in slope-intercept form.

\newline

2x + 3y < -6

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Write the following inequality in slope-intercept form.

\newline

-7x - y \geq 21

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 8 months ago

Question

Write the following inequality in slope-intercept form.

\newline

5x - 4y > -20

\newline

Write your answer with

y

first, followed by an inequality symbol. Use integers, proper fractions, and improper fractions in simplest form.

Posted 9 months ago

Question

Miyoko's goal is to earn more than

(950

this week. She earns

)250

for every day she works as a cryptographer, and earns

\$180

for every day she works as a geologist.

\newline

Write an inequality that represents the number of days Miyoko should work as a cryptographer

C

and as a geologist

G

to achieve her goal.

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant