Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

V=pir^(2)h
The formula gives the volume
V of a right circular cylinder with radius
r and height
h. What is the volume, in cubic inches, of a right circular cylinder with a radius of 3 inches and a height of 2 inches?
Choose 1 answer:
(A)
5pi
(B)
6pi
(c)
12 pi
(D)
18 pi

$V=\pi r^{2} h$ $\newline$ The formula gives the volume $V$ of a right circular cylinder with radius $r$ and height $h$ . What is the volume, in cubic inches, of a right circular cylinder with a radius of $3$ inches and a height of $2$ inches? $\newline$ Choose $1$ answer: $\newline$ (A) $5 \pi$ $\newline$ (B) $6 \pi$ $\newline$ (C) $12 \pi$ $\newline$ (D) $18 \pi$

View step-by-step help

View step-by-step help

Write equations of sine and cosine functions using properties

Full solution

Q.

V=\pi r^{2} h

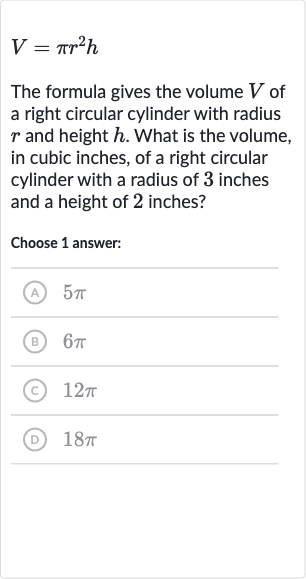
\newline

The formula gives the volume

V

of a right circular cylinder with radius

r

and height

h

. What is the volume, in cubic inches, of a right circular cylinder with a radius of

3

inches and a height of

2

inches?

\newline

Choose

1

answer:

\newline

(A)

5 \pi

\newline

(B)

6 \pi

\newline

(C)

12 \pi

\newline

(D)

18 \pi

Identify values for radius and height: Identify the given values for the radius $r$ and height $h$ of the cylinder. $\newline$ Radius $r = 3$ inches $\newline$ Height $h = 2$ inches $\newline$ The formula for the volume $V$ of a right circular cylinder is $V = \pi r^2 h$ .
Substitute values into formula: Substitute the given values into the volume formula. $V = \pi \times (3 \, \text{inches})^2 \times (2 \, \text{inches})$
Calculate radius squared: Calculate the radius squared. $\newline$ $(3 \text{ inches})^2 = 9 \text{ square inches}$
Multiply base area by height: Multiply the area of the base by the height to find the volume. $V = \pi \times 9 \text{ square inches} \times 2 \text{ inches}$
Simplify expression to find volume: Simplify the expression to find the volume. $\newline$ $V = \pi \times 9 \times 2$ $\newline$ $V = 18\pi$ cubic inches

More problems from Write equations of sine and cosine functions using properties

Question

Find an equation for a sinusoidal function that has period

2\pi

1

, and contains the point

\left(\pi, -1\right)

\newline

Write your answer in the form

f(x)=A\cos(Bx+C)+D

A

B

C

D

are real numbers.

\newline

f(x)=

Posted 1 month ago

Question

Find an equation for a sinusoidal function that has period

2\pi

1

, and contains the point

\left(-\frac{\pi}{2},-1\right)

. Write your answer in the form

f(x) = A\sin(Bx + C) + D

A

B

C

D

are real numbers. `f(x)` =______

Posted 3 months ago

Question

Find an equation for a sinusoidal function that has period

2\pi

1

, and contains the point

(0,-1)

\newline

Write your answer in the form

f(x) = A\cos(Bx + C) + D

A

B

C

D

are real numbers.

\newline

f(x) =

Posted 2 months ago

Question

Franklin Middle School is having a canned food drive. In Mr. Lao's class, Mr. Lao brought

10

cans of food, and each student brought

2

cans. In Ms. Roger's class, Ms. Rogers did not bring any cans, but each student brought

3

cans of food. Write two equations in slope-intercept form to represent the number of cans of food for each class

y

in terms of the number of students

x

Posted 2 months ago

Question

Franklin Middle School is having a canned food drive. In Mr. Lao's class, Mr. Lao brought

10

cans of food, and each student brought

2

cans. In Ms. Roger's class, Ms. Rogers did not bring any cans, but each student brought

3

cans of food. Write two equations in slope-intercept form to represent the number of cans of food for each class

y

in terms of the number of students

x

Posted 2 months ago

Question

Kris is wrapping Christmas lights around the railing that runs around three sides of his square porch If one side of his porch is

12

feet long, and each strand of his Christmes lights will wrap around a

70

-inch length of the railing, what is the minimum number of strands Kris needs to completely wrap the porch railing?

\newline

6

\newline

7

\newline

8

\newline

9

Posted 2 months ago

Question

Kris is wrapping Christmas lights around the railing that runs around three sides of his square porch If one side of his porch is

12

feet long, and each strand of his Christmas lights will wrap around a

70

-inch length of the railing, what is the minimum number of strands Kris needs to completely wrap the porch railing?

\newline

6

\newline

7

\newline

8

\newline

9

Posted 2 months ago

Question

For a given input value

b

f

outputs a value

a

to satisfy the following equation.

\newline

4a+7b=-52

\newline

Write a formula for

f(b)

b

\newline

f(b)=\square

Posted 2 months ago

Question

For a given input value

x

g

outputs a value

y

to satisfy the following equation.

\newline

-4x-6=-5y+2

\newline

Write a formula for

g(x)

x

\newline

g(x)=\square

Posted 4 months ago

Question

For a given input value

a

f

outputs a value

b

to satisfy the following equation.

\newline

-3a+6b=a+4b

\newline

Write a formula for

f(a)

a

\newline

f(a)=\square

Posted 4 months ago