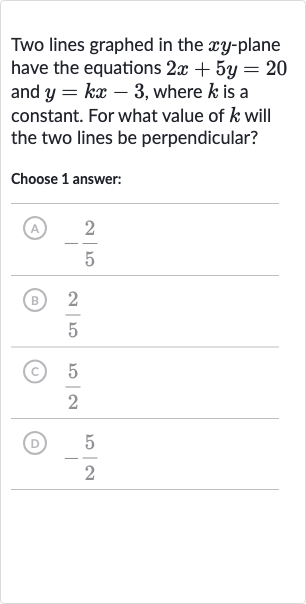
Two lines graphed in the xy-plane have the equations 2x+5y=20 and y=kx-3, where k is a constant. For what value of k will the two lines be perpendicular? Choose 1 answer: (A) -(2)/(5) (B) (2)/(5) (C) (5)/(2) (D) -(5)/(2)

Question

Two lines graphed in the  xy-plane have the equations  2x+5y=20 and  y=kx-3, where  k is a constant. For what value of  k will the two lines be perpendicular? Choose 1 answer: (A)  -(2)/(5) (B)  (2)/(5) (C)  (5)/(2) (D)  -(5)/(2)

Bytelearn · Accepted Answer

Find slope of first line: Find the slope of the first line. The equation of the first line is 2x + 5y = 20. To find the slope, we need to rewrite this equation in slope-intercept form, which is y = mx + b, where m is the slope.Rewrite first equation in slope-intercept form: Rewrite the first equation in slope-intercept form. Subtract 2x from both sides to get 5y = -2x + 20. Then divide by 5 to isolate y, yielding y = (-2/5)x + 4. The slope of the first line is -2/5.Determine slope of second line: Determine the slope of the second line that would make it perpendicular to the first line. Since the slopes of perpendicular lines are opposite reciprocals, we take the negative reciprocal of -2/5 to find the slope of the second line. The negative reciprocal of -2/5 is 5/2.Compare slope to given options: Compare the slope of the second line to the given options. The slope of the second line is 5/2, which corresponds to option (C) 5/2.

Full solution

More problems from Slopes of parallel and perpendicular lines

Related topics