Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

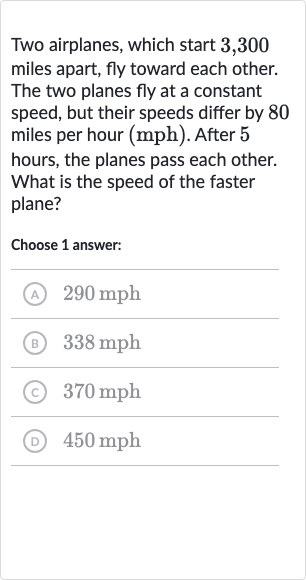
Two airplanes, which start 3,300 miles apart, fly toward each other. The two planes fly at a constant speed, but their speeds differ by 80 miles per hour (mph). After 5 hours, the planes pass each other. What is the speed of the faster plane?
Choose 1 answer:
(A)
290mph
(B)
338mph
(c)
370mph
(D)
450mph

Two airplanes, which start $3$ , $300$ miles apart, fly toward each other. The two planes fly at a constant speed, but their speeds differ by $80$ miles per hour (mph). After $5$ hours, the planes pass each other. What is the speed of the faster plane? $\newline$ Choose $1$ answer: $\newline$ (A) $290 \mathrm{mph}$ $\newline$ (B) $338 \mathrm{mph}$ $\newline$ (C) $370 \mathrm{mph}$ $\newline$ (D) $450 \mathrm{mph}$

View step-by-step help

View step-by-step help

Experimental probability

Full solution

Q. Two airplanes, which start

3

,

300

miles apart, fly toward each other. The two planes fly at a constant speed, but their speeds differ by

80

miles per hour (mph). After

5

hours, the planes pass each other. What is the speed of the faster plane?

\newline

Choose

1

answer:

\newline

(A)

290 \mathrm{mph}

\newline

(B)

338 \mathrm{mph}

\newline

(C)

370 \mathrm{mph}

\newline

(D)

450 \mathrm{mph}

Denote Speeds: Let's denote the speed of the slower plane as $S$ mph and the speed of the faster plane as $S + 80$ mph. Since they are flying towards each other, their relative speed is the sum of their individual speeds.
Calculate Relative Speed: The relative speed of the two planes is $S + (S + 80)$ mph, which simplifies to $2S + 80$ mph.
Use Distance Formula: In $5$ hours, the distance covered by the two planes together at their relative speed is equal to the initial distance between them, which is $3,300$ miles. So, we can write the equation: $(2S + 80) \times 5 = 3,300$ .
Solve for S: Solving the equation for S, we get $2S + 80 = 660$ (since $3,300 / 5 = 660$ ).
Subtract $80$ : Subtracting $80$ from both sides of the equation gives us $2S = 660 - 80$ , which simplifies to $2S = 580$ .
Find Faster Plane Speed: Dividing both sides of the equation by $2$ gives us $S = \frac{580}{2}$ , which simplifies to $S = 290 \, \text{mph}$ . This is the speed of the slower plane.
Find Faster Plane Speed: Dividing both sides of the equation by $2$ gives us $S = \frac{580}{2}$ , which simplifies to $S = 290$ mph. This is the speed of the slower plane.To find the speed of the faster plane, we add $80$ mph to the speed of the slower plane: $290$ mph + $80$ mph = $370$ mph.

More problems from Experimental probability

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. ____ `%`

Posted 2 months ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 3 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 2 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 3 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 2 months ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 3 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 3 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 3 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 3 months ago