Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

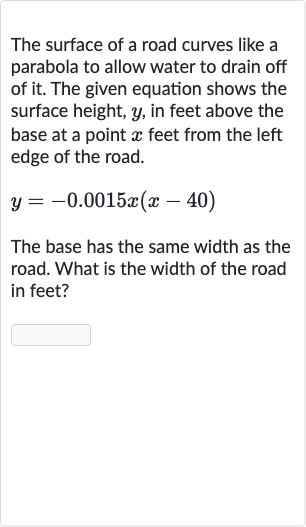
The surface of a road curves like a parabola to allow water to drain off of it. The given equation shows the surface height,
y, in feet above the base at a point
x feet from the left edge of the road.

y=-0.0015 x(x-40)
The base has the same width as the road. What is the width of the road in feet?

The surface of a road curves like a parabola to allow water to drain off of it. The given equation shows the surface height, $y$ , in feet above the base at a point $x$ feet from the left edge of the road. $\newline$ $y=-0.0015 x(x-40)$ $\newline$ The base has the same width as the road. What is the width of the road in feet?

View step-by-step help

View step-by-step help

Scale drawings: word problems

Full solution

Q. The surface of a road curves like a parabola to allow water to drain off of it. The given equation shows the surface height,

y

, in feet above the base at a point

x

feet from the left edge of the road.

\newline

y=-0.0015 x(x-40)

\newline

The base has the same width as the road. What is the width of the road in feet?

Identify x-intercepts: Identify the x-intercepts of the parabola to determine the width of the road. $\newline$ The equation of the parabola is given by $y = -0.0015 x(x - 40)$ . The x-intercepts occur when $y = 0$ . $\newline$ $0 = -0.0015 x(x - 40)$
Solve equation for x: Solve the equation for $x$ to find the $x$ -intercepts. $\newline$ We can factor out $x$ from the equation: $\newline$ $0 = x(-0.0015 x + 0.0015 \times 40)$ $\newline$ $0 = x(-0.0015 x + 0.06)$ $\newline$ The $x$ -intercepts are $x = 0$ and $x = 40$ .
Determine road width: Determine the width of the road using the x-intercepts. $\newline$ The width of the road is the distance between the two x-intercepts. Since the x-intercepts are $0$ and $40$ , the width of the road is $40$ feet.

More problems from Scale drawings: word problems

Question

Eric made a scale drawing of the auditorium. The stage, which is \(35\) feet wide in real life, is \(5\) inches wide in the drawing. What is the scale of the drawing? \(1\) inch :

\_\_\_\_\_

Posted 5 months ago

Question

\newline

66

=

\_\_\_\_\_

Posted 5 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 5 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 5 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 5 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 5 months ago

Question

Wyatt, a chemist at a chemical supply company, has carefully measured out

100

gallons of a solution containing

14\%

acetone. He also has access to unlimited quantities of a

9\%

acetone solution. How many gallons of the

9\%

acetone solution must Wyatt add to the

14\%

acetone solution to create a solution that contains

10\%

\newline

Write your answer as a whole number or as a decimal rounded to the nearest tenth.

\newline

\newline

\newline

Posted 5 months ago

Question

William recently started running after school. Yesterday, he ran

4.8

41

6

seconds. Today, he ran

4.1

33

4

seconds. What was William's average speed over the two runs?

\newline

Write your answer as a whole number, a decimal, or a simplified fraction or mixed number. Do not round.

\newline

\newline

____ miles per minute

\newline

Posted 7 months ago

Question

\newline

750

=

Posted 7 months ago

Question

\newline

250

=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant