AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
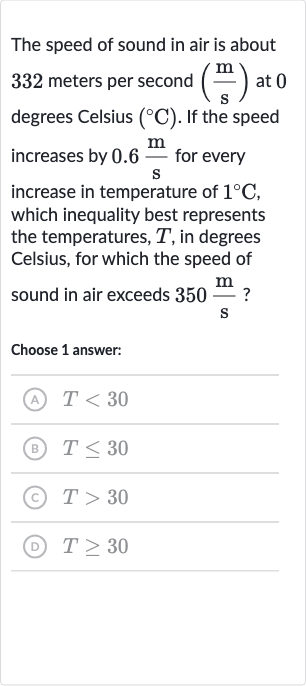
The speed of sound in air is about meters per second at degrees Celsius . If the speed increases by for every increase in temperature of , which inequality best represents the temperatures, , in degrees Celsius, for which the speed of sound in air exceeds ?Choose answer:(A) T<30 (B) (C) T>30 (D)
Full solution
Q. The speed of sound in air is about meters per second at degrees Celsius . If the speed increases by for every increase in temperature of , which inequality best represents the temperatures, , in degrees Celsius, for which the speed of sound in air exceeds ?Choose answer:(A) (B) (C) (D)
- Given Information: We are given that the speed of sound in air at degrees Celsius is meters per second. We are also told that the speed increases by meters per second for every degree Celsius increase in temperature. We need to find the temperature at which the speed of sound exceeds meters per second. Let's denote the temperature in degrees Celsius as .
- Expression Setup: First, we need to set up an equation that relates the speed of sound to the temperature. The speed of sound at any temperature can be represented as , where is the speed of sound at degrees Celsius and is the increase in speed for degrees above degrees Celsius.
- Inequality Setup: Next, we want to find the value of for which the speed of sound exceeds meters per second. This means we need to solve the inequality 332 + 0.6T > 350.
- Subtract : To solve for , we subtract from both sides of the inequality: 0.6T > 350 - 332
- Perform Subtraction: Performing the subtraction gives us 0.6T > 18.
- Divide by .: Now, we divide both sides of the inequality by to solve for : T > \frac{18}{0.6}
- Final Result: Dividing by gives us T > 30. Therefore, the inequality that represents the temperatures for which the speed of sound in air exceeds meters per second is T > 30.
More problems from Write a linear inequality: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
