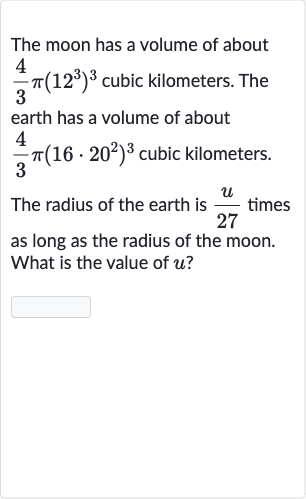
The moon has a volume of about (4)/(3)pi(12^(3))^(3) cubic kilometers. The earth has a volume of about (4)/(3)pi(16*20^(2))^(3) cubic kilometers. The radius of the earth is (u)/( 27) times as long as the radius of the moon. What is the value of u ?

Question

The moon has a volume of about  (4)/(3)pi(12^(3))^(3) cubic kilometers. The earth has a volume of about  (4)/(3)pi(16*20^(2))^(3) cubic kilometers. The radius of the earth is  (u)/( 27) times as long as the radius of the moon. What is the value of  u ?

Bytelearn · Accepted Answer

Denote Radii: Let's denote the radius of the moon as r_moon and the radius of the earth as r_earth. According to the given information, r_earth = (u/27) * r_moon. We are given the volumes of the moon and the earth in terms of their radii. We need to find the value of u.Volume Calculations: The volume of a sphere is given by the formula V = (4/3)πr^3. The volume of the moon is given as (4/3)π(12^3)^3 cubic kilometers. Let's simplify this expression. V_moon = (4/3)π(12^3)^3 = (4/3)π(12^3 * 12^3 * 12^3)Volume Equations: Now, let's simplify the expression for the volume of the moon further. V_moon = (4/3)π(12^3 * 12^3 * 12^3) = (4/3)π(12^9)Solve for u^3: Similarly, the volume of the earth is given as (4/3)π(16*20^2)^3 cubic kilometers. Let's simplify this expression. V_earth = (4/3)π(16*20^2)^3 = (4/3)π(16^3 * 20^6)Simplify Equation: Now, let's simplify the expression for the volume of the earth further. V_earth = (4/3)π(16^3 * 20^6) = (4/3)π(16^3 * 20^6)Calculate u: We know that the volume of the earth is related to the volume of the moon by the cube of their radius ratio. So, we can set up the following equation: (4/3)π(r_earth^3) = (4/3)π(16^3 * 20^6) (4/3)π(r_moon^3) = (4/3)π(12^9)Since the volumes are proportional to the cube of their radii, we can equate the two expressions by their corresponding radii: r_earth^3 = 16^3 * 20^6 r_moon^3 = 12^9Now, we can express r_earth in terms of r_moon using the given relationship r_earth = (u/27) * r_moon. Substituting this into the equation for r_earth^3, we get: ((u/27) * r_moon)^3 = 16^3 * 20^6Expanding the left side of the equation, we have: (u^3/27^3) * r_moon^3 = 16^3 * 20^6We know that r_moon^3 = 12^9, so we can substitute this into the equation: (u^3/27^3) * 12^9 = 16^3 * 20^6Now, we can solve for u^3 by isolating it on one side of the equation: u^3 = (27^3 * 16^3 * 20^6) / 12^9Before we calculate u^3, let's simplify the equation by canceling out common factors. We can simplify 16^3 and 12^9 by noting that 16 = 2^4 and 12 = 2^2 * 3, so 16^3 = (2^4)^3 and 12^9 = (2^2 * 3)^9. u^3 = (27^3 * (2^4)^3 * 20^6) / ((2^2 * 3)^9)Simplifying further, we get: u^3 = (27^3 * 2^12 * 20^6) / (2^18 * 3^9)Now, we can cancel out the common factors of 2 and 3 from the numerator and denominator: u^3 = (27^3 * 2^12 * 20^6) / (2^18 * 3^9) u^3 = (3^9 * 2^12 * (2^2 * 10)^6) / (2^18 * 3^9) u^3 = (2^12 * 2^12 * 10^6) / 2^18After canceling out the common factors, we have: u^3 = (2^24 * 10^6) / 2^18 u^3 = 2^6 * 10^6Now, we can calculate u^3: u^3 = 2^6 * 10^6 = 64 * 10^6To find u, we take the cube root of both sides: u = (64 * 10^6)^(1/3)Calculating the cube root, we get: u = 4 * 10^2 u = 400

The moon has a volume of about $\frac{4}{3} \pi\left(12^{3}\right)^{3}$ cubic kilometers. The earth has a volume of about $\frac{4}{3} \pi\left(16 \cdot 20^{2}\right)^{3}$ cubic kilometers. The radius of the earth is $\frac{u}{27}$ times as long as the radius of the moon. What is the value of $u$ ?

Full solution

More problems from Scale drawings: word problems

Related topics