Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

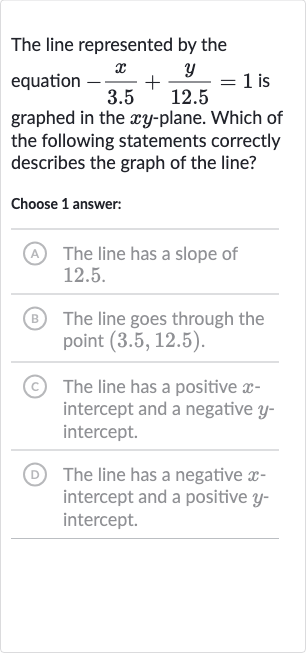
The line represented by the equation -(x)/( 3.5)+(y)/( 12.5)=1 is graphed in the xy-plane. Which of the following statements correctly describes the graph of the line? Choose 1 answer: (A) The line has a slope of 12.5. (B) The line goes through the point (3.5,12.5). (C) The line has a positive x intercept and a negative y intercept. (D) The line has a negative x intercept and a positive y intercept.

The line represented by the equation −x3.5+y12.5=1 -\frac{x}{3.5}+\frac{y}{12.5}=1 is graphed in the xy x y -plane. Which of the following statements correctly describes the graph of the line?\newlineChoose 11 answer:\newline(A) The line has a slope of 1212.55 .\newline(B) The line goes through the point (3.5,12.5) (3.5,12.5) .\newline(C) The line has a positive x x intercept and a negative y y intercept.\newline(D) The line has a negative x x intercept and a positive y y intercept.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Slopes of parallel and perpendicular linesright chevron icon

Full solution

Q. The line represented by the equation −x3.5+y12.5=1 -\frac{x}{3.5}+\frac{y}{12.5}=1 is graphed in the xy x y -plane. Which of the following statements correctly describes the graph of the line?\newlineChoose 11 answer:\newline(A) The line has a slope of 1212.55 .\newline(B) The line goes through the point (3.5,12.5) (3.5,12.5) .\newline(C) The line has a positive x x intercept and a negative y y intercept.\newline(D) The line has a negative x x intercept and a positive y y intercept.
  1. Convert equation to slope-intercept form: Convert the given equation to slope-intercept form y=mx+by = mx + b.\newlineThe given equation is: −x3.5+y12.5=1-\frac{x}{3.5} + \frac{y}{12.5} = 1\newlineMultiply through by 3.5×12.53.5 \times 12.5 to clear the denominators:\newline−12.5x+3.5y=3.5×12.5-12.5x + 3.5y = 3.5 \times 12.5
  2. Isolate y in the equation: Isolate y on one side of the equation.\newline3.5y=12.5x+3.5×12.53.5y = 12.5x + 3.5 \times 12.5\newlineDivide by 3.53.5 to solve for y:\newliney=12.53.5x+12.5y = \frac{12.5}{3.5}x + 12.5
  3. Simplify the equation: Simplify the equation.\newliney=12.53.5x+12.5y = \frac{12.5}{3.5}x + 12.5\newliney=257x+12.5y = \frac{25}{7}x + 12.5\newlineThis is the slope-intercept form of the equation, where the slope (mm) is 257\frac{25}{7} and the y-intercept (bb) is 12.512.5.
  4. Analyze slope and y-intercept: Analyze the slope and y-intercept. The slope is positive, which means the line rises from left to right. The y-intercept is positive, which means the line crosses the y-axis above the origin.
  5. Determine x-intercept: Determine the x-intercept.\newlineTo find the x-intercept, set yy to 00 in the equation and solve for xx:\newline0=257x+12.50 = \frac{25}{7}x + 12.5\newline257x=−12.5\frac{25}{7}x = -12.5\newlinex=−12.5/257x = -12.5 / \frac{25}{7}\newlinex=−12.5×725x = -12.5 \times \frac{7}{25}\newlinex=−3.5x = -3.5\newlineThe x-intercept is −3.5-3.5, which means it is negative.
  6. Choose correct statement: Choose the correct statement based on the analysis.\newline(A) The line has a slope of 12.512.5. (Incorrect, the slope is 257\frac{25}{7})\newline(B) The line goes through the point (3.5,12.5)(3.5,12.5). (Incorrect, this is not the xx-intercept or yy-intercept)\newline(C) The line has a positive xx-intercept and a negative yy-intercept. (Incorrect, the xx-intercept is negative and the yy-intercept is positive)\newline(D) The line has a negative xx-intercept and a positive yy-intercept. (Correct, based on our calculations)

More problems from Slopes of parallel and perpendicular lines

Question
Does the point (0,4)(0, 4) satisfy the equation y=xy = x??
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the slope of the line y=−4x+25 y = -4x + \frac{2}{5} .
Get tutor helpright-arrow

Posted 9 months ago

Question
Rewrite the following equation in slope-intercept form.\newliney+8=−8(x−10)y + 8 = -8(x - 10)
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the y y -intercept of the line 14x−16y=−10 14x - 16y = -10 .\newlineWrite your answer as an integer or decimal or fraction, not as an ordered pair.
Get tutor helpright-arrow

Posted 9 months ago

Question
Line q q has a slope of −23 \frac{-2}{3} . Line r r is perpendicular to q q . What is the slope of line r r ?
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the slope of the line y+3=−118(x+6)y + 3 = -\frac{1}{18}(x + 6).\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Line p p has an equation of y=−8x+6 y = -8x + 6 . Line q q , which is perpendicular to line p p , includes the point (2,−2) (2, -2) . What is the equation of line q q ??\newlineWrite the equation in slope-intercept form.
Get tutor helpright-arrow

Posted 9 months ago

Question
Is the graph of this equation a horizontal or vertical line?\newlinex=7x = 7
Get tutor helpright-arrow

Posted 9 months ago

Question
Determine the standard form of the following equation:\newliney=−10x+7 y = -10x + 7
Get tutor helpright-arrow

Posted 9 months ago

Question
A line with a slope of 99 passes through the point (9,9)(9,9). What is its equation in point-slope form?
Get tutor helpright-arrow

Posted 9 months ago

View all (99)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant