Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

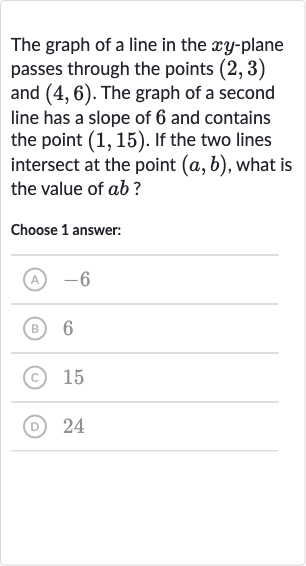
The graph of a line in the xy-plane passes through the points (2,3) and (4,6). The graph of a second line has a slope of 6 and contains the point (1,15). If the two lines intersect at the point (a,b), what is the value of ab ? Choose 1 answer: (A) -6 (B) 6 (C) 15 (D) 24

The graph of a line in the xy x y -plane passes through the points (2,3) (2,3) and (4,6) (4,6) . The graph of a second line has a slope of 66 and contains the point (1,15) (1,15) . If the two lines intersect at the point (a,b) (a, b) , what is the value of ab a b ?\newlineChoose 11 answer:\newline(A) −6-6\newline(B) 66\newline(C) 1515\newline(D) 2424

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Slopes of parallel and perpendicular linesright chevron icon

Full solution

Q. The graph of a line in the xy x y -plane passes through the points (2,3) (2,3) and (4,6) (4,6) . The graph of a second line has a slope of 66 and contains the point (1,15) (1,15) . If the two lines intersect at the point (a,b) (a, b) , what is the value of ab a b ?\newlineChoose 11 answer:\newline(A) −6-6\newline(B) 66\newline(C) 1515\newline(D) 2424
  1. Find Slope: First, find the slope of the line passing through the points (2,3)(2,3) and (4,6)(4,6).\newlineSlope (m)=(y2−y1)(x2−x1)=(6−3)(4−2)=32(m) = \frac{(y_2 - y_1)}{(x_2 - x_1)} = \frac{(6 - 3)}{(4 - 2)} = \frac{3}{2}
  2. Write Equation: Next, use the point-slope form to write the equation of the first line.\newliney−y1=m(x−x1)y - y_1 = m(x - x_1), where mm is the slope and (x1,y1)(x_1, y_1) is a point on the line.\newlineUsing the point (2,3)(2,3) and the slope 32\frac{3}{2}, the equation becomes:\newliney−3=(32)(x−2)y - 3 = \left(\frac{3}{2}\right)(x - 2)
  3. Simplify Equation: Simplify the equation of the first line to get it in slope-intercept form y=mx+by = mx + b.y−3=(32)x−3y - 3 = \left(\frac{3}{2}\right)x - 3y=(32)xy = \left(\frac{3}{2}\right)x
  4. Write Second Line: Now, write the equation of the second line using its slope and the given point (1,15)(1,15). The slope is 66, and using the point-slope form: y−y1=m(x−x1)y - y_1 = m(x - x_1) y−15=6(x−1)y - 15 = 6(x - 1)
  5. Simplify Second Line: Simplify the equation of the second line to get it in slope-intercept form.\newliney−15=6x−6y - 15 = 6x - 6\newliney=6x+9y = 6x + 9
  6. Find Intersection Point: To find the intersection point (a,b)(a,b), set the yy-values of the two equations equal to each other since they both equal yy at the point of intersection.(32)x=6x+9\left(\frac{3}{2}\right)x = 6x + 9
  7. Solve for x: Solve for x by getting all terms involving xx on one side and constants on the other.32x−6x=9\frac{3}{2}x - 6x = 9Multiply all terms by 22 to clear the fraction:3x−12x=183x - 12x = 18
  8. Combine Like Terms: Combine like terms to solve for xx.−9x=18-9x = 18x=18−9x = \frac{18}{-9}x=−2x = -2
  9. Find y-coordinate: Now that we have the x-coordinate of the intersection point, we can find the y-coordinate by plugging xx into one of the line equations. We'll use the first line's equation.y=(32)xy = \left(\frac{3}{2}\right)xy=(32)(−2)y = \left(\frac{3}{2}\right)(-2)y=−3y = -3
  10. Intersection Point: The intersection point (a,b)(a,b) is (−2,−3)(-2,-3). To find the value of abab, multiply aa and bb together.\newlineab=(−2)(−3)ab = (-2)(-3)\newlineab=6ab = 6

More problems from Slopes of parallel and perpendicular lines

Question
Does the point (0,4)(0, 4) satisfy the equation y=xy = x??
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the slope of the line y=−4x+25 y = -4x + \frac{2}{5} .
Get tutor helpright-arrow

Posted 9 months ago

Question
Rewrite the following equation in slope-intercept form.\newliney+8=−8(x−10)y + 8 = -8(x - 10)
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the y y -intercept of the line 14x−16y=−10 14x - 16y = -10 .\newlineWrite your answer as an integer or decimal or fraction, not as an ordered pair.
Get tutor helpright-arrow

Posted 9 months ago

Question
Line q q has a slope of −23 \frac{-2}{3} . Line r r is perpendicular to q q . What is the slope of line r r ?
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the slope of the line y+3=−118(x+6)y + 3 = -\frac{1}{18}(x + 6).\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Line p p has an equation of y=−8x+6 y = -8x + 6 . Line q q , which is perpendicular to line p p , includes the point (2,−2) (2, -2) . What is the equation of line q q ??\newlineWrite the equation in slope-intercept form.
Get tutor helpright-arrow

Posted 9 months ago

Question
Is the graph of this equation a horizontal or vertical line?\newlinex=7x = 7
Get tutor helpright-arrow

Posted 9 months ago

Question
Determine the standard form of the following equation:\newliney=−10x+7 y = -10x + 7
Get tutor helpright-arrow

Posted 9 months ago

Question
A line with a slope of 99 passes through the point (9,9)(9,9). What is its equation in point-slope form?
Get tutor helpright-arrow

Posted 9 months ago

View all (99)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant