AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
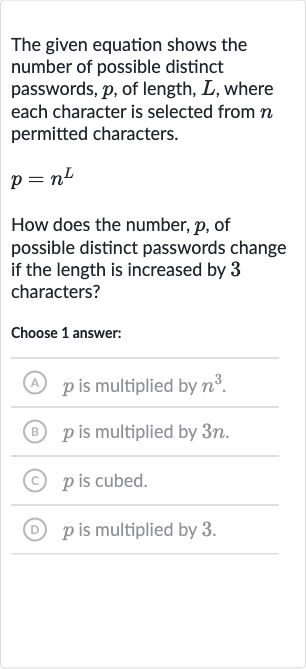
The given equation shows the number of possible distinct passwords, , of length, , where each character is selected from permitted characters.How does the number, , of possible distinct passwords change if the length is increased by characters?Choose answer:(A) is multiplied by .(B) is multiplied by .(C) is cubed.(D) is multiplied by .
Full solution
Q. The given equation shows the number of possible distinct passwords, , of length, , where each character is selected from permitted characters.How does the number, , of possible distinct passwords change if the length is increased by characters?Choose answer:(A) is multiplied by .(B) is multiplied by .(C) is cubed.(D) is multiplied by .
- Understand Formula Explanation: Understand the original formula for the number of possible distinct passwords. The formula given is , where is the number of possible passwords, is the number of permitted characters, and is the length of the password.
- Determine New Password Length: Determine the new length of the password after increasing it by characters.If the original length is , the new length will be .
- Apply New Length to Formula: Apply the new length to the formula to find the new number of possible passwords. The new number of possible passwords will be .
- Express New Passwords in Terms: Express the new number of possible passwords in terms of the original number of possible passwords.Using the properties of exponents, we can rewrite as .Since , we can substitute into the equation to get .
- Compare with Answer Choices: Compare the new expression with the answer choices.The expression matches with answer choice (A), which states that is multiplied by .
