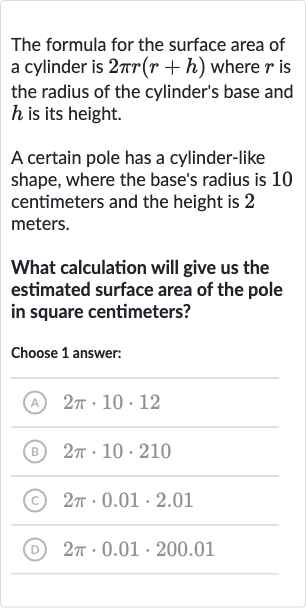
The formula for the surface area of a cylinder is $\newline$ $2\pi r(r+h)$ where $\newline$ $r$ is the radius of the cylinder's base and $\newline$ $h$ is its height. $\newline$ A certain pole has a cylinder-like shape, where the base's radius is $10$ centimeters and the height is $2$ meters. $\newline$ What calculation will give us the estimated surface area of the pole in square centimeters? $\newline$ Choose $1$ answer: $\newline$ (A) $2\pi \cdot 10 \cdot 12$ $\newline$ (B) $2\pi \cdot 10 \cdot 210$ $\newline$ (C) $2\pi \cdot 0.01 \cdot 2.01$ $\newline$ (D) $2\pi \cdot 0.01 \cdot 200.01$

Full solution

Q. The formula for the surface area of a cylinder is

\newline

2\pi r(r+h)

where

\newline

r

is the radius of the cylinder's base and

\newline

h

is its height.

\newline

A certain pole has a cylinder-like shape, where the base's radius is

10

centimeters and the height is

2

meters.

\newline

What calculation will give us the estimated surface area of the pole in square centimeters?

\newline

Choose

1

answer:

\newline

(A)

2\pi \cdot 10 \cdot 12

\newline

(B)

2\pi \cdot 10 \cdot 210

\newline

(C)

2\pi \cdot 0.01 \cdot 2.01

\newline

(D)

2\pi \cdot 0.01 \cdot 200.01

Identify Given Values: Identify the given values for the radius and height of the cylinder. The radius $r$ is $10$ centimeters, and the height $h$ is given in meters, so it needs to be converted to centimeters. $\newline$ Height in meters = $2$ m $\newline$ Convert meters to centimeters: $1$ m = $100$ cm $\newline$ Height in centimeters = $2$ m $*$ $100$ cm/m = $200$ cm
Write Formula: Write down the formula for the surface area of a cylinder: Surface Area = $2 \pi r (r + h)$ .
Substitute Values: Substitute the given values into the formula: Surface Area $= 2 \times \pi \times 10 \, \text{cm} \times (10 \, \text{cm} + 200 \, \text{cm})$ .
Simplify Expression: Simplify the expression inside the parentheses: $10\,\text{cm} + 200\,\text{cm} = 210\,\text{cm}.$
Calculate Surface Area: Now, substitute the simplified expression back into the formula: Surface Area = $2 \times \pi \times 10 \, \text{cm} \times 210 \, \text{cm}$ .
Identify Correct Answer: Identify the correct answer from the given options. The calculation that matches our formula is (B) $2\pi\cdot 10\cdot 210$ .