Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

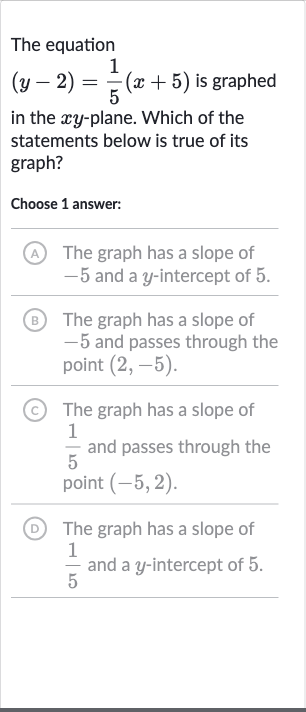
The equation (y-2)=(1)/(5)(x+5) is graphed in the xy-plane. Which of the statements below is true of its graph? Choose 1 answer: A The graph has a slope of -5 and a y-intercept of 5 . (B) The graph has a slope of -5 and passes through the point (2,-5). (C) The graph has a slope of (1)/(5) and passes through the point (-5,2). D The graph has a slope of (1)/(5) and a y-intercept of 5 .

The equation\newline(y−2)=15(x+5) (y-2)=\frac{1}{5}(x+5) is graphed in the xy x y -plane. Which of the statements below is true of its graph?\newlineChoose 11 answer:\newline(A) The graph has a slope of −5-5 and a y y -intercept of 55 .\newline(B) The graph has a slope of −5-5 and passes through the point (2,−5) (2,-5) .\newline(C) The graph has a slope of 15 \frac{1}{5} and passes through the point (−5,2) (-5,2) .\newlineD The graph has a slope of 15 \frac{1}{5} and a y y -intercept of 55 .

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Slopes of parallel and perpendicular linesright chevron icon

Full solution

Q. The equation\newline(y−2)=15(x+5) (y-2)=\frac{1}{5}(x+5) is graphed in the xy x y -plane. Which of the statements below is true of its graph?\newlineChoose 11 answer:\newline(A) The graph has a slope of −5-5 and a y y -intercept of 55 .\newline(B) The graph has a slope of −5-5 and passes through the point (2,−5) (2,-5) .\newline(C) The graph has a slope of 15 \frac{1}{5} and passes through the point (−5,2) (-5,2) .\newlineD The graph has a slope of 15 \frac{1}{5} and a y y -intercept of 55 .
  1. Identify slope and intercepts: We need to identify the slope and intercepts of the given equation to determine which statement is true. The equation is given in a form that is close to slope-intercept form, which is y=mx+by = mx + b, where mm is the slope and bb is the yy-intercept.
  2. Rewrite equation in slope-intercept form: First, let's rewrite the equation in slope-intercept form by isolating yy on one side of the equation.y−2=(15)(x+5)y - 2 = \left(\frac{1}{5}\right)(x + 5)Add 22 to both sides to isolate yy.y=(15)(x+5)+2y = \left(\frac{1}{5}\right)(x + 5) + 2
  3. Distribute and combine terms: Now, let's distribute the (15)(\frac{1}{5}) across the terms inside the parentheses.\newliney=(15)x+(15)⋅5+2y = (\frac{1}{5})x + (\frac{1}{5})\cdot5 + 2\newliney=(15)x+1+2y = (\frac{1}{5})x + 1 + 2
  4. Simplify the equation: Combine the constant terms to find the y-intercept.\newliney=15x+3y = \frac{1}{5}x + 3\newlineThis equation tells us that the slope (mm) is 15\frac{1}{5} and the y-intercept (bb) is 33.
  5. Compare findings with answer choices: Now, let's compare our findings with the answer choices.\newlineA) Incorrect, because the slope is not −5-5 and the y-intercept is not 55.\newlineB) Incorrect, because the slope is not −5-5 and it does not pass through the point (2,−5)(2, -5).\newlineC) Correct, because the slope is 15\frac{1}{5} and the equation passes through the point (−5,2)(-5, 2).\newlineD) Incorrect, because the y-intercept is not 55, it is 33.
  6. Final Answer: True statement is: \newlineC) The graph has a slope of 15 \frac{1}{5} and passes through the point (−5,2) (-5,2) .

More problems from Slopes of parallel and perpendicular lines

Question
Does the point (0,4)(0, 4) satisfy the equation y=xy = x??
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the slope of the line y=−4x+25 y = -4x + \frac{2}{5} .
Get tutor helpright-arrow

Posted 9 months ago

Question
Rewrite the following equation in slope-intercept form.\newliney+8=−8(x−10)y + 8 = -8(x - 10)
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the y y -intercept of the line 14x−16y=−10 14x - 16y = -10 .\newlineWrite your answer as an integer or decimal or fraction, not as an ordered pair.
Get tutor helpright-arrow

Posted 9 months ago

Question
Line q q has a slope of −23 \frac{-2}{3} . Line r r is perpendicular to q q . What is the slope of line r r ?
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the slope of the line y+3=−118(x+6)y + 3 = -\frac{1}{18}(x + 6).\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Line p p has an equation of y=−8x+6 y = -8x + 6 . Line q q , which is perpendicular to line p p , includes the point (2,−2) (2, -2) . What is the equation of line q q ??\newlineWrite the equation in slope-intercept form.
Get tutor helpright-arrow

Posted 9 months ago

Question
Is the graph of this equation a horizontal or vertical line?\newlinex=7x = 7
Get tutor helpright-arrow

Posted 9 months ago

Question
Determine the standard form of the following equation:\newliney=−10x+7 y = -10x + 7
Get tutor helpright-arrow

Posted 9 months ago

Question
A line with a slope of 99 passes through the point (9,9)(9,9). What is its equation in point-slope form?
Get tutor helpright-arrow

Posted 9 months ago

View all (99)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant