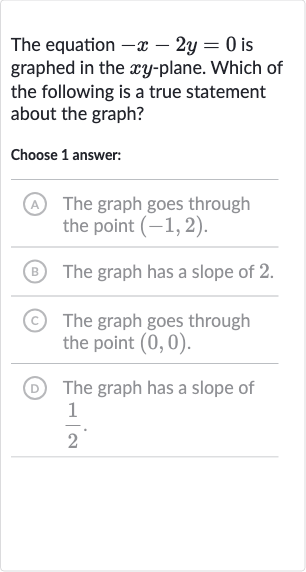
The equation -x-2y=0 is graphed in the xy-plane. Which of the following is a true statement about the graph? Choose 1 answer: A The graph goes through the point (-1,2). (B) The graph has a slope of 2. (C) The graph goes through the point (0,0). (D) The graph has a slope of (1)/(2).

Question

The equation  -x-2y=0 is graphed in the  xy-plane. Which of the following is a true statement about the graph? Choose 1 answer: A The graph goes through the point  (-1,2). (B) The graph has a slope of 2. (C) The graph goes through the point  (0,0). (D) The graph has a slope of  (1)/(2).

Bytelearn · Accepted Answer

Rewrite Equation: First, we need to rewrite the equation in slope-intercept form, which is y = mx + b, where m is the slope and b is the y-intercept. The given equation is -x - 2y = 0. To rewrite it, we solve for y: -2y = x y = (-1/2)xIdentify Slope and Y-Intercept: Now that we have the equation in slope-intercept form, we can identify the slope and y-intercept. The slope (m) is -1/2, and the y-intercept (b) is 0 since there is no constant added to the mx term.Evaluate Answer Choices (A): We can now evaluate the answer choices based on the slope-intercept form of the equation: (A) The graph goes through the point (-1,2). To check this, we can substitute x = -1 and y = 2 into the equation y = (-1/2)x and see if it holds true: 2 = (-1/2)(-1) 2 = 1/2 This is not true, so option (A) is incorrect.Evaluate Answer Choices (B): (B) The graph has a slope of 2. We have already determined that the slope is -1/2, so option (B) is incorrect.Evaluate Answer Choices (C): (C) The graph goes through the point (0,0). To check this, we can substitute x = 0 and y = 0 into the equation y = (-1/2)x: 0 = (-1/2)(0) 0 = 0 This is true, so option (C) is a possible correct answer.Evaluate Answer Choices (D): (D) The graph has a slope of (1)/(2). We have already determined that the slope is -1/2, not 1/2, so option (D) is incorrect.

Full solution

More problems from Slopes of parallel and perpendicular lines

Related topics