Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for
x.

5x-29 > -34quad OR
quad2x+31 < 29
Choose 1 answer:
(A)
x < -1 or
x > -1
(B)
x < -1
(C)
x > -1
(D) There are no solutions
(E) All values of
x are solutions

Solve for $x$ . $\newline$ $5 x-29>-34 \quad$ OR $\quad 2 x+31<29$ $\newline$ Choose $1$ answer: $\newline$ (A) $x<-1$ or $x>-1$ $\newline$ (B) $x<-1$ $\newline$ (C) $x>-1$ $\newline$ (D) There are no solutions $\newline$ (E) All values of $x$ are solutions

View step-by-step help

View step-by-step help

Solve polynomial equations

Full solution

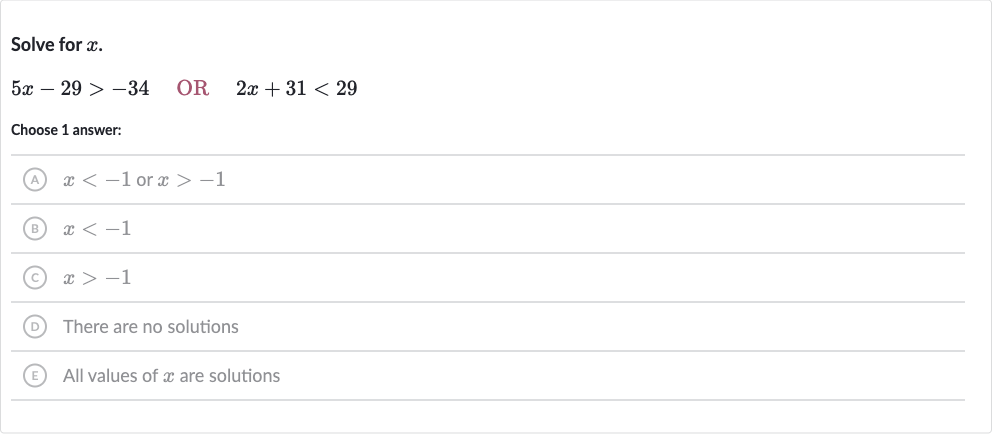
Q. Solve for

x

.

\newline

5 x-29>-34 \quad

OR

\quad 2 x+31<29

\newline

Choose

1

answer:

\newline

(A)

x<-1

or

x>-1

\newline

(B)

x<-1

\newline

(C)

x>-1

\newline

(D) There are no solutions

\newline

(E) All values of

x

are solutions

Solve first inequality: Solve the first inequality $5x - 29 > -34$ . $\newline$ Add $29$ to both sides of the inequality to isolate the term with $x$ . $\newline$ $5x - 29 + 29 > -34 + 29$ $\newline$ $5x > -5$ $\newline$ Now, divide both sides by $5$ to solve for $x$ . $\newline$ $\frac{5x}{5} > \frac{-5}{5}$ $\newline$ $x > -1$
Isolate term with x: Solve the second inequality $2x + 31 < 29$ .
Subtract $31$ from both sides of the inequality to isolate the term with $x$ .
$2x + 31 - 31 < 29 - 31$
$2x < -2$
Now, divide both sides by $2$ to solve for $x$ .
$\frac{2x}{2} < \frac{-2}{2}$
$x < -1$
Divide both sides by $5$ : Combine the solutions of both inequalities. $\newline$ The first inequality gives us $x > -1$ . $\newline$ The second inequality gives us $x < -1$ . $\newline$ Since these are two separate conditions connected by an ＂OR＂, the solution set includes all $x$ that satisfy either condition. $\newline$ Therefore, the solution set is $x < -1$ OR $x > -1$ .

More problems from Solve polynomial equations

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 3 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 3 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 3 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 3 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 3 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 3 months ago