Full solution
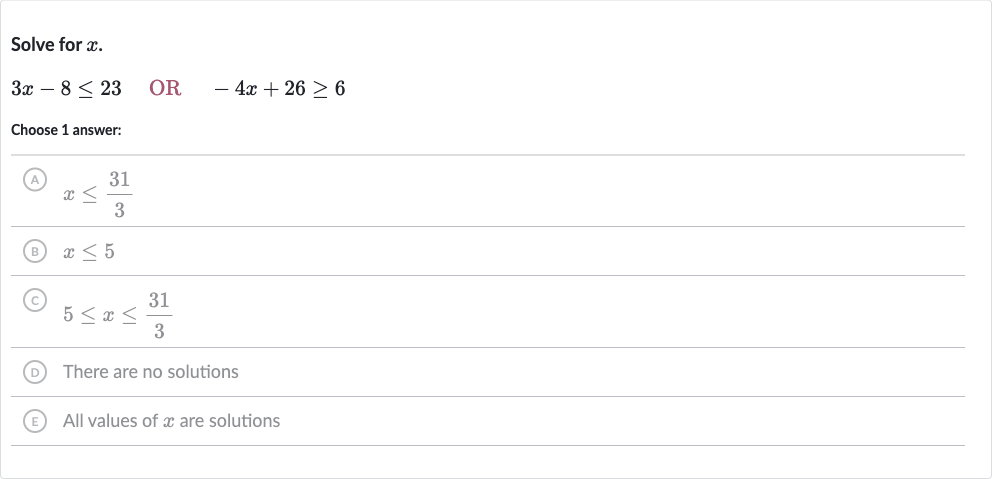
Q. Solve for . OR Choose answer:(A) (B) (C) (D) There are no solutionsㄷ) All values of are solutions
- Solve First Inequality: First, let's solve the inequality . To isolate , we need to add to both sides of the inequality. Now, divide both sides by to solve for .
- Solve Second Inequality: Next, let's solve the inequality . To isolate , we need to subtract from both sides of the inequality. Now, divide both sides by to solve for . Remember that dividing by a negative number reverses the inequality sign.
- Combine Inequalities: Now we have two inequalities from the compound inequality: from the first inequality, and from the second inequality. Since the original problem states "OR" between the two inequalities, we need to find the union of the solutions. The union of and is all that satisfy either one or both of the inequalities. Since is less than , the solution that encompasses both is .
More problems from Is (x, y) a solution to the system of linear inequalities?
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help