Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

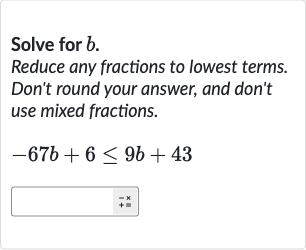
$Solve for b. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions. -67 b+6 <= 9b+43$

Solve for $b$ . Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions. $\newline$ $-67b + 6 \leq 9b + 43$

View step-by-step help

View step-by-step help

Solve multi-step inequalities

Full solution

Q. Solve for

b

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

-67b + 6 \leq 9b + 43

Isolate variable b: First, we need to isolate the variable $b$ on one side of the inequality. To do this, we will add $67b$ to both sides to move all the $b$ terms to the right side. $\newline$ $-67b + 6 + 67b \leq 9b + 43 + 67b$ $\newline$ This simplifies to: $\newline$ $6 \leq 76b + 43$
Subtract to isolate term: Next, we subtract $43$ from both sides to isolate the term with $b$ on the right side. $\newline$ $6 - 43 \leq 76b + 43 - 43$ $\newline$ This simplifies to: $\newline$ $-37 \leq 76b$
Divide to solve for b: Now, we divide both sides by $76$ to solve for $b$ . $\newline$ $-\frac{37}{76} \leq \frac{76b}{76}$ $\newline$ This simplifies to: $\newline$ $-\frac{37}{76} \leq b$
Reduce fraction $-\frac{37}{76}$ : We can reduce the fraction $-\frac{37}{76}$ to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor, which is $1$ in this case. So the fraction is already in its lowest terms. $\newline$ $-\frac{37}{76} \leq b$

More problems from Solve multi-step inequalities

Question

w

\newline

\frac{w}{-1} + 7 > 9

\newline

Posted 9 months ago

Question

u

\newline

6.4u < 3.84 + 6.8u

\newline

\newline

Write your answer with

u

first, followed by an inequality symbol.

\newline

\newline

Posted 9 months ago

Question

t

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

12t - 2 < -5t + 36

Posted 8 months ago

Question

m

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

8m + 95 < -87m + 5

Posted 10 months ago

Question

r

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

35r-21 < -35r+19

Posted 10 months ago

Question

x

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

54x + 64 \geq 49x + 59

Posted 10 months ago

Question

w

.\ Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

53w+13 < 56w+16

Posted 10 months ago

Question

p

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

-7p - 4 > 26p - 94

Posted 10 months ago

Question

d

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

-23d + 81 \leq -98d + 1

Posted 10 months ago

Question

b

. Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions.

\newline

30b + 53 \geq 18b - 83

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant