Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

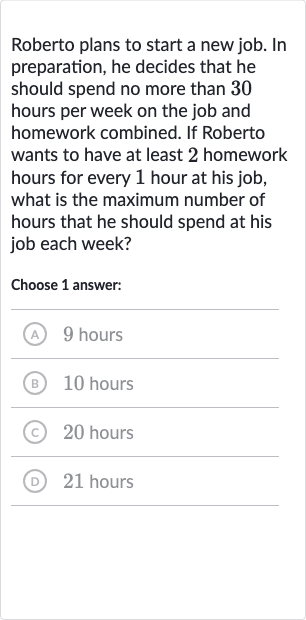
Roberto plans to start a new job. In preparation, he decides that he should spend no more than 30 hours per week on the job and homework combined. If Roberto wants to have at least 2 homework hours for every 1 hour at his job, what is the maximum number of hours that he should spend at his job each week?
Choose 1 answer:
(A) 9 hours
(B) 10 hours
(c) 20 hours
(D) 21 hours

Roberto plans to start a new job. In preparation, he decides that he should spend no more than $30$ hours per week on the job and homework combined. If Roberto wants to have at least $2$ homework hours for every $1$ hour at his job, what is the maximum number of hours that he should spend at his job each week? $\newline$ Choose $1$ answer: $\newline$ (A) $9$ hours $\newline$ (B) $10$ hours $\newline$ (C) $20$ hours $\newline$ (D) $21$ hours

View step-by-step help

View step-by-step help

Counting principle

Full solution

Q. Roberto plans to start a new job. In preparation, he decides that he should spend no more than

30

hours per week on the job and homework combined. If Roberto wants to have at least

2

homework hours for every

1

hour at his job, what is the maximum number of hours that he should spend at his job each week?

\newline

Choose

1

answer:

\newline

(A)

9

hours

\newline

(B)

10

hours

\newline

(C)

20

hours

\newline

(D)

21

hours

Denoting hours for job and homework: Let's denote the number of hours Roberto spends at his job as $J$ and the number of hours he spends on homework as $H$ . According to the problem, Roberto wants to spend at least $2$ hours on homework for every hour at his job. This can be written as: $\newline$ $H = 2J$
Total hours constraint: We also know that the total number of hours spent on the job and homework combined should not exceed $30$ hours per week. This can be expressed as: $\newline$ $J + H \leq 30$
Substituting equations: Substituting the first equation $H = 2J$ into the second equation $J + H \leq 30$ , we get: $J + 2J \leq 30$
Combining like terms: Combining like terms, we have: $3J \leq 30$
Dividing the inequality: To find the maximum number of hours Roberto can spend at his job, we divide both sides of the inequality by $3$ : $\newline$ $J \leq \frac{30}{3}$
Calculating the maximum hours: Calculating the division, we get: $\newline$ $J \leq 10$
Calculating the maximum hours: Calculating the division, we get: $\newline$ $J \leq 10$ Therefore, the maximum number of hours Roberto should spend at his job each week is $10$ hours.

More problems from Counting principle

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage.

\newline

Posted 5 months ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 9 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 8 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 9 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 7 months ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 9 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 8 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 9 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 9 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant