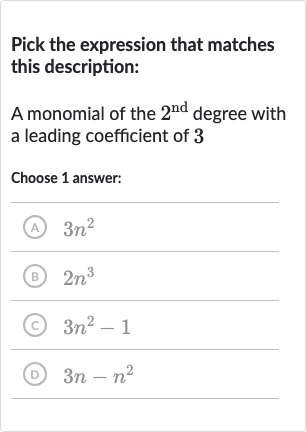
Pick the expression that matches this description: A monomial of the 2^("nd ") degree with a leading coefficient of 3 Choose 1 answer: (A) 3n^(2) (B) 2n^(3) (C) 3n^(2)-1 (D) 3n-n^(2)

Question

Pick the expression that matches this description: A monomial of the  2^("nd ") degree with a leading coefficient of 3 Choose 1 answer: (A)  3n^(2) (B)  2n^(3) (C)  3n^(2)-1 (D)  3n-n^(2)

Bytelearn · Accepted Answer

Definition of a monomial: A monomial is a single term algebraic expression. The 2nd degree indicates that the variable should have an exponent of 2. The leading coefficient is the number in front of the variable with the highest power, which should be 3 in this case.Analysis of option (A): Option (A) 3n^2 is a monomial because it has a single term. It is of the 2nd degree because the exponent of n is 2. The leading coefficient is 3. This matches the description.Analysis of option (B): Option (B) 2n^3 is a monomial, but it is of the 3rd degree because the exponent of n is 3, and the leading coefficient is 2, not 3. This does not match the description.Analysis of option (C): Option (C) 3n^2-1 is not a monomial because it consists of two terms, 3n^2 and -1. Even though the first term has the correct degree and leading coefficient, the presence of the second term disqualifies it.Analysis of option (D): Option (D) 3n-n^2 is not a monomial because it has two terms, 3n and -n^2. Additionally, the term with the highest degree has a coefficient of -1, not 3. This does not match the description.

Pick the expression that matches this description: $\newline$ A monomial of the $2^{\text {nd }}$ degree with a leading coefficient of $3$ $\newline$ Choose $1$ answer: $\newline$ (A) $3 n^{2}$ $\newline$ (B) $2 n^{3}$ $\newline$ (C) $3 n^{2}-1$ $\newline$ (D) $3 n-n^{2}$

Full solution

More problems from Multiply a polynomial by a monomial

Related topics

Pick the expression that matches this description:\newlineA monomial of the 2nd 2^{\text {nd }} 2nd degree with a leading coefficient of 333\newlineChoose 111 answer:\newline(A) 3n2 3 n^{2} 3n2\newline(B) 2n3 2 n^{3} 2n3\newline(C) 3n2−1 3 n^{2}-1 3n2−1\newline(D) 3n−n2 3 n-n^{2} 3n−n2

Pick the expression that matches this description: $\newline$ A monomial of the $2^{\text {nd }}$ degree with a leading coefficient of $3$ $\newline$ Choose $1$ answer: $\newline$ (A) $3 n^{2}$ $\newline$ (B) $2 n^{3}$ $\newline$ (C) $3 n^{2}-1$ $\newline$ (D) $3 n-n^{2}$