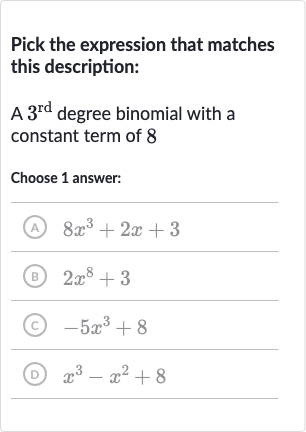
Pick the expression that matches this description: A 3^("rd ") degree binomial with a constant term of 8 Choose 1 answer: (A) 8x^(3)+2x+3 (B) 2x^(8)+3 (C) -5x^(3)+8 (D) x^(3)-x^(2)+8

Question

Pick the expression that matches this description: A  3^("rd ") degree binomial with a constant term of 8 Choose 1 answer: (A)  8x^(3)+2x+3 (B)  2x^(8)+3 (C)  -5x^(3)+8 (D)  x^(3)-x^(2)+8

Bytelearn · Accepted Answer

Identify 3rd Degree Binomial: The question prompt is asking us to identify a 3rd degree binomial with a constant term of 8.Definition of 3rd Degree Binomial: A 3rd degree binomial means that the highest power of the variable (usually x) in the expression should be 3, and there should be two terms in the expression.Constant Term of 8: A constant term is a term that does not contain any variables, just a number. We are looking for a constant term of 8.Evaluation of Options: Let's evaluate each option: (A) 8x^(3)+2x+3 - This is not a binomial because it has three terms, not two.Option (A): (B) 2x^(8)+3 - This is not a 3rd degree expression because the highest power of x is 8, not 3. Also, it is not a binomial.Option (B): (C) -5x^(3)+8 - This is a binomial because it has two terms, and it is a 3rd degree expression because the highest power of x is 3. The constant term is 8.Option (C): (D) x^(3)-x^(2)+8 - This is not a binomial because it has three terms, not two.Option (D): The expression that matches the description of a 3rd degree binomial with a constant term of 8 is option (C) -5x^(3)+8.

Pick the expression that matches this description: $\newline$ A $3^{\text {rd }}$ degree binomial with a constant term of $8$ $\newline$ Choose $1$ answer: $\newline$ (A) $8 x^{3}+2 x+3$ $\newline$ (B) $2 x^{8}+3$ $\newline$ (C) $-5 x^{3}+8$ $\newline$ (D) $x^{3}-x^{2}+8$

Full solution

More problems from Multiply a polynomial by a monomial

Related topics