AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
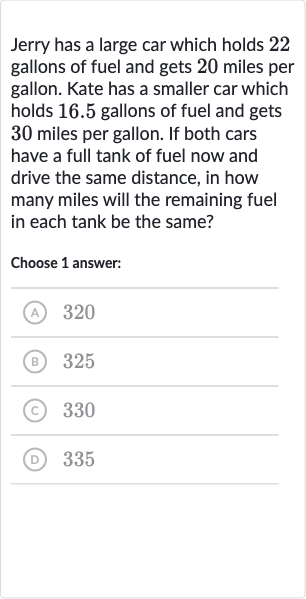
Jerry has a large car which holds gallons of fuel and gets miles per gallon. Kate has a smaller car which holds . gallons of fuel and gets miles per gallon. If both cars have a full tank of fuel now and drive the same distance, in how many miles will the remaining fuel in each tank be the same?Choose answer:(A) (B) (C) (D)
Full solution
Q. Jerry has a large car which holds gallons of fuel and gets miles per gallon. Kate has a smaller car which holds . gallons of fuel and gets miles per gallon. If both cars have a full tank of fuel now and drive the same distance, in how many miles will the remaining fuel in each tank be the same?Choose answer:(A) (B) (C) (D)
- Set up an equation based on the fuel consumption: Let be the number of miles driven.For Jerry's car: Fuel consumption rate: miles per gallon Initial fuel: gallons For Kate's car: Fuel consumption rate: miles per gallon Initial fuel: gallons Setting up the equation:
- Isolating the term : Add to both sides of the equation: Subtract from both sides:
- Simplify the equation: To simplify, let's find a common denominator, which is :
- Solving for the value of : To solve for multiply both sides of the equation by : The remaining fuel in each tank will be the same in miles.
More problems from Mean, median, mode, and range
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
