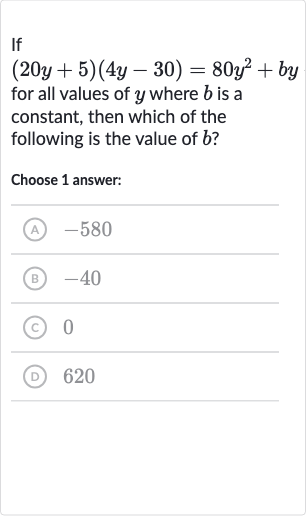
If (20 y+5)(4y-30)=80y^(2)+by for all values of y where b is a constant, then which of the following is the value of b ? Choose 1 answer: (A) -580 (B) -40 (c) 0 (D) 620

Question

If  (20 y+5)(4y-30)=80y^(2)+by for all values of  y where  b is a constant, then which of the following is the value of  b ? Choose 1 answer: (A) -580 (B) -40 (c) 0 (D) 620

Bytelearn · Accepted Answer

Expand left side using distributive property: First, we will expand the left side of the equation using the distributive property (also known as the FOIL method for binomials). (20y + 5)(4y - 30) = 80y^2 + by Expanding gives us: 20y * 4y + 20y * (-30) + 5 * 4y + 5 * (-30)Perform multiplication for each term: Now, we will perform the multiplication for each term. 20y * 4y = 80y^2 20y * (-30) = -600y 5 * 4y = 20y 5 * (-30) = -150 So, the expanded form is: 80y^2 - 600y + 20y - 150Combine like terms on the left side: Next, we combine like terms on the left side of the equation. 80y^2 - 600y + 20y - 150 = 80y^2 + by Combining the y terms gives us: 80y^2 - 580y - 150 = 80y^2 + byEquating coefficients of y: Since the equation must hold for all values of y, the coefficients of the corresponding y terms on both sides of the equation must be equal. This means that the coefficient of y on the left side must be equal to b on the right side. Therefore, -580y = byFind the value of b: We can now equate the coefficients of y from both sides to find the value of b. -580 = bWe have found the value of b, which is -580. This corresponds to answer choice (A).

If $\newline$ $(20 y+5)(4 y-30)=80 y^{2}+b y$ $\newline$ for all values of $y$ where $b$ is a constant, then which of the following is the value of $b$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $-580$ $\newline$ (B) $-40$ $\newline$ (C) $0$ $\newline$ (D) $620$

Full solution

More problems from Solve multi-step equations with fractional coefficients

Related topics