Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the sum of the first 8 terms in the following geometric series. Do not round your answer. 2+8+32+dots

Find the sum of the first 88 terms in the following geometric series. Do not round your answer.\newline2+8+32+… 2+8+32+\ldots

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Distance between two pointsright chevron icon

Full solution

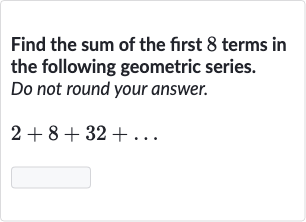
Q. Find the sum of the first 88 terms in the following geometric series. Do not round your answer.\newline2+8+32+… 2+8+32+\ldots
  1. Identifying the first term and common ratio: To find the sum of the first 88 terms of a geometric series, we need to identify the first term (aa) and the common ratio (rr) of the series. The first term is given as 22. To find the common ratio, we divide the second term by the first term.\newlineCalculation: r=82=4r = \frac{8}{2} = 4
  2. Using the formula for the sum of the first n terms: Now that we have the first term (a = 22) and the common ratio (r = 44), we can use the formula for the sum of the first n terms of a geometric series: S_n = \frac{a(11 - r^n)}{11 - r}, where n is the number of terms.\newlineWe want to find the sum of the first 88 terms, so n = 88.
  3. Substituting values into the formula: Plugging the values into the formula, we get S8=2(1−48)1−4S_8 = \frac{2(1 - 4^8)}{1 - 4}.\newlineCalculation: S8=2(1−48)1−4S_8 = \frac{2(1 - 4^8)}{1 - 4}
  4. Calculating 484^8: Before we continue, let's calculate 484^8 to avoid any math errors later on.\newlineCalculation: 48=655364^8 = 65536
  5. Substituting 484^8 into the formula: Now we substitute 484^8 into the formula.\newlineCalculation: S8=2(1−65536)1−4S_8 = \frac{2(1 - 65536)}{1 - 4}
  6. Simplifying the expression: Simplify the expression inside the parentheses.\newlineCalculation: S8=2(−65535)−3S_8 = \frac{2(-65535)}{-3}
  7. Calculating the sum of the first 88 terms: Now we divide −65535-65535 by −3-3 and multiply by 22 to find the sum of the first 88 terms.\newlineCalculation: S8=2×655353=2×21845=43690S_8 = 2 \times \frac{65535}{3} = 2 \times 21845 = 43690

More problems from Distance between two points

Question
if −5,6 -5,6 is reflected in the line y=−x y=-x then rotated 180∘ 180^\circ about the point −7,2 -7,2 what are the coordinate?
Get tutor helpright-arrow

Posted 1 year ago

Question
Find the xx- and yy-intercepts for the graph of the following equation.\newliney=13x−4y=\frac{1}{3}x-4
Get tutor helpright-arrow

Posted 1 year ago

Question
The midpoint MM of VW‾\overline{VW} has coordinates (8, 5)(8,\,5). Point VV has coordinates (10, 2)(10,\,2). Find the coordinates of point WW.\newlineWrite the coordinates as decimals or integers.\newlineW=(_, _)W = (\_,\,\_)
Get tutor helpright-arrow

Posted 1 year ago

Question
The midpoint of VW‾\overline{VW} is M(3, 3)M(3,\,3). One endpoint is V(4, 6)V(4,\,6). Find the coordinates of the other endpoint WW.\newlineWrite the coordinates as decimals or integers.\newlineW=(_, _)W = (\_,\,\_)
Get tutor helpright-arrow

Posted 1 year ago

Question
The midpoint MM of VW‾\overline{VW} has coordinates (9, 4)(9,\,4). Point WW has coordinates (10, 8)(10,\,8). Find the coordinates of point VV.\newlineWrite the coordinates as decimals or integers.\newlineV=(_, _)V = (\_,\,\_)
Get tutor helpright-arrow

Posted 1 year ago

Question
The midpoint MM of GH‾\overline{GH} has coordinates (5, 3)(5,\,3). Point HH has coordinates (5, 4)(5,\,4). Find the coordinates of point GG.\newlineWrite the coordinates as decimals or integers.\newlineG=(_, _)G = (\_,\,\_)
Get tutor helpright-arrow

Posted 1 year ago

Question
Highlight the preposition in the sentence below.\newlineAt the music festival, Taylor McKessie played her new accordion.
Get tutor helpright-arrow

Posted 8 months ago

Question
You pick a card at random, put it back, and then pick another card at random.\newline44\newline55\newline66\newline77\newlineWhat is the probability of picking a number greater than 55 and then picking a 44 ?\newlineWrite your answer as a percentage.
Get tutor helpright-arrow

Posted 6 months ago

Question
Jeanne's bank account earns interest annually. The equation shows her starting balance of $500\$500 and her balance at the end of three years, $546.36\$546.36. At what rate rr did Jeanne earn interest?\newline546.36=500(1+r)546.36 = 500(1 + r)
Get tutor helpright-arrow

Posted 6 months ago

Question
Jeanne's bank account earns interest annually. The equation shows her starting balance of $350 \$ 350 and her balance at the end of three years, $422.78 \$ 422.78 . At what rate r did Jeanne earn interest?\newline422.78=350(1+r)3422.78=350(1+r)^{3}
Get tutor helpright-arrow

Posted 6 months ago

View all (1)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant