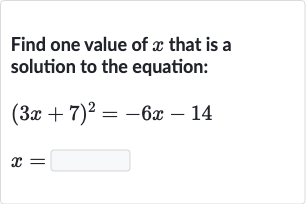Full solution
Q. Find one value of that is a solution to the equation:
- Write Equation: Write down the given equation.
- Expand Equation: Expand the left side of the equation.Combine like terms.
- Combine Like Terms: Move all terms to one side to set the equation to zero.Combine like terms.
- Move Terms to One Side: Factor the quadratic equation.We need to find two numbers that multiply to and add up to .The numbers and already satisfy this condition.
- Factor Quadratic Equation: Solve for x by setting each factor equal to zero. or For the first factor:For the second factor:
- Solve for x: Check the solutions in the original equation.For : (True)For : (True)Both solutions are valid.
More problems from Solve a quadratic equation by factoring
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help