Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

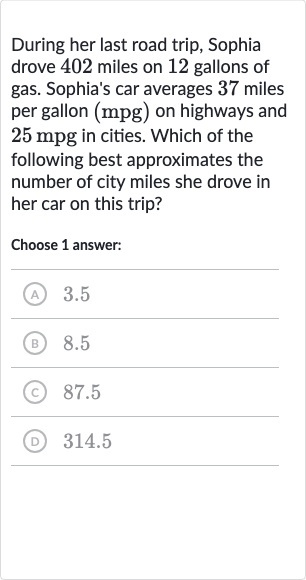
During her last road trip, Sophia drove 402 miles on 12 gallons of gas. Sophia's car averages 37 miles per gallon
(mpg) on highways and
25mpg in cities. Which of the following best approximates the number of city miles she drove in her car on this trip?
Choose 1 answer:
(A) 3.5
(B) 8.5
(C) 87.5
(D) 314.5

During her last road trip, Sophia drove $402$ miles on $12$ gallons of gas. Sophia's car averages $37$ miles per gallon $(\mathrm{mpg})$ on highways and $25 \mathrm{mpg}$ in cities. Which of the following best approximates the number of city miles she drove in her car on this trip? $\newline$ Choose $1$ answer: $\newline$ (A) $3$ . $5$ $\newline$ (B) $8$ . $5$ $\newline$ (C) $87$ . $5$ $\newline$ (D) $314$ . $5$

View step-by-step help

View step-by-step help

Multi-step problems with unit conversions

Full solution

Q. During her last road trip, Sophia drove

402

miles on

12

gallons of gas. Sophia's car averages

37

miles per gallon

(\mathrm{mpg})

on highways and

25 \mathrm{mpg}

in cities. Which of the following best approximates the number of city miles she drove in her car on this trip?

\newline

Choose

1

answer:

\newline

(A)

3

.

5

\newline

(B)

8

.

5

\newline

(C)

87

.

5

\newline

(D)

314

.

5

Problem Understanding: Distance Sophia drove on total trip: $402 \text{ miles}$ $\newline$ Total gas for the trip: $12 \text{ gallons}$ $\newline$ Highway gas mileage = $37 \text{ mpg}$ $\newline$ City gas mileage = $25 \text{ mpg}$ $\newline$ Let $G$ = gallons used in city $\newline$ Then, $12 - G$ = gallons used in highway
Mileage formula: $\text{Gas mileage} = \frac{\text{Distance driven in miles}}{\text{Number of gallons of gas consumed}}$ $\newline$ Let $m = \text{gas mileage}$ , $d = \text{distance}$ , $g = \text{gallons of gas}$ . $\newline$ So the formula becomes $m = \frac{d}{g}$ $\newline$ Solve the mileage equation for distance: $\newline$ $d = mg$
Setting up the equation: We know that the total miles drove = $402$ $\newline$ Let, $x = \text{number of city miles}$ ; and $y = \text{number of highway miles}$ . $\newline$ So, $x + y = 402$ . $\newline$ Distance in City: $\newline$ $d=mg$ $\newline$ $x=25G$ $\newline$ Distance in Highway: $\newline$ $d=mg$ $\newline$ $y=37(12-G)$ $\newline$ Now, we have a system of 3 equations: $\newline$ $x + y = 402$ $\newline$ $x=25G$ $\newline$ $y=37(12-G)$
Solve for the value $G$ : Substitute the values of $x$ and $y$ in terms of $G$ in $x + y = 402$ . $\newline$ $25G + 37(12-G) = 402$ $\newline$ $25G + 444 - 37G = 402$ $\newline$ Combine like terms in left side: $\newline$ $444 - 12G = 402$ $\newline$ Subtract $444$ on both sides: $\newline$ $- 12G = -42$ $\newline$ Divide both sides by $-12$ to solve for $G$ . $\newline$ $G = \frac{-42}{-12}$ $\newline$ $G = \frac{7}{2} = 3.5$
Final Solution: Sophia used $3.5 \text{ gallons}$ in the city. $\newline$ $d=mg$ $\newline$ $d=25 \times 3.5$ $\newline$ $d=87.5$ $\newline$ Sophia drove $87.5 \text{ miles}$ in the city.

More problems from Multi-step problems with unit conversions

Question

Eric made a scale drawing of the auditorium. The stage, which is \(35\) feet wide in real life, is \(5\) inches wide in the drawing. What is the scale of the drawing? \(1\) inch :

\_\_\_\_\_

Posted 1 month ago

Question

\newline

66

=

\_\_\_\_\_

Posted 1 month ago

Question

Wyatt, a chemist at a chemical supply company, has carefully measured out

100

gallons of a solution containing

14\%

acetone. He also has access to unlimited quantities of a

9\%

acetone solution. How many gallons of the

9\%

acetone solution must Wyatt add to the

14\%

acetone solution to create a solution that contains

10\%

\newline

Write your answer as a whole number or as a decimal rounded to the nearest tenth.

\newline

\newline

\newline

Posted 1 month ago

Question

William recently started running after school. Yesterday, he ran

4.8

41

6

seconds. Today, he ran

4.1

33

4

seconds. What was William's average speed over the two runs?

\newline

Write your answer as a whole number, a decimal, or a simplified fraction or mixed number. Do not round.

\newline

\newline

____ miles per minute

\newline

Posted 1 month ago

Question

\newline

750

=

Posted 1 month ago

Question

\newline

250

=

Posted 1 month ago

Question

An electrolyte solution has an average current density of

1\,\frac{\text{A}}{\text{dm}^2}

\newline

What is the current density of the solution in

\frac{\text{A}}{\text{m}^2}

\newline

\square

\frac{\text{A}}{\text{m}^2}

Posted 1 month ago

Question

The formula for the length of the hypotenuse in a right triangle is

\sqrt{a^{2}+b^{2}}

a

b

are the lengths of the triangle's sides (this formula is derived from the Pythagorean theorem).

\newline

From the side, a certain ramp has a right-triangular shape. Its height is

30

centimeters and its horizontal length is

3

\newline

What calculation will give us the estimated length of the ramp in meters?

\newline

1

\newline

\sqrt{\left(\frac{30^{2}}{100^{2}}\right)+3^{2}}

\newline

\sqrt{30^{2}+3^{2}\cdot 100^{2}}

\newline

\sqrt{30^{2}\cdot 100^{2}+3^{2}}

\newline

\sqrt{30^{2}+\left(\frac{3^{2}}{100^{2}}\right)}

Posted 1 month ago

Question

Roselyn is driving to visit her family, who live

150

kilometers away. Her average speed is

60

kilometers per hour. The car's tank has

20

liters of fuel at the beginning of the drive, and its fuel efficiency is

6

kilometers per liter. Fuel costs

0.60

dollars per liter.

\newline

What is the price for the amount of fuel that Roselyn will use for the entire drive?

\newline

Posted 1 month ago

Question

David is making rice for his guests based on a recipe that requires rice, water, and a special blend of spice, where the rice-to-spice ratio is

15 : 1

. He currently has

40

grams of the spice blend, and he can go buy more if necessary. He wants to make

10

servings, where each serving has

75

grams of rice. Overall, David spends

4.50

dollars on rice.

\newline

How many servings can David make with the current amount of spice he has?

\newline

\square

Posted 28 days ago